Single peaked preferences

Single-peaked preferences are a class of preference relations. A group of agents is said to have single-peaked preferences over a set of possible outcomes if the outcomes can be ordered along a line such that:

1. Each agent has a "best outcome" in the set, and -
2. For each agent, outcomes that are further from his best outcome are preferred less.

Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied.

With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome: it is to select the median quantity. See the median voter theorem. It is truthful because the median function satisfies the strong monotonicity property.

The notion was first presented by Duncan Black[1] and later by Kenneth Arrow.[2]

Definitions

Let ${\displaystyle X=\{x_{1},\ldots ,x_{m}\}}$ be the set of possible outcomes. Let ${\displaystyle N=\{1,\ldots ,n\}}$ be the set of agents. The preference-relation of agent i is denoted by ${\displaystyle \succ _{i}}$. The maximum element of ${\displaystyle \succ _{i}}$ in X is denoted by ${\displaystyle x_{i}^{*}}$_.

Definition using a common order

The group N is said to have single-peaked preferences over X, if there exists an ordering > of the outcomes such that, for every agent i in N:

${\displaystyle x_{k}<x_{j}\leq x_{i}^{*}\Rightarrow x_{j}\succ _{i}x_{k}}$ ${\displaystyle x_{k}>x_{j}\geq x_{i}^{*}\Rightarrow x_{j}\succ _{i}x_{k}}$

In words, ${\displaystyle x_{i}^{*}}$ is the ideal point for agent i. When the agent compares between two outcomes that are both to the right or to the left of his ideal point, he strictly prefers whichever option is closest to ${\displaystyle x_{i}^{*}}$.

Note that the preference-relations ${\displaystyle \succ _{i}}$ are different, but the ordering > of the outcomes must be the same for all agents.

Definition using triplets

Ballester and Haeringer[3] proved the following characterization of single-peaked preferences, which can be seen as an alternative definition.

The group N is said to have single-peaked preferences over X, if for every triplet of outcomes in X, there exists an outcome that is not ranked last by any agent in N.

Some examples

Single-peaked preferences

The following graph shows a set of three preferences that are single-peaked over outcomes {A,B,C,D,E}. On the vertical axis, the number represents the preference ranking of the outcome, with 1 being most preferred. Two outcomes that are equally preferred have the same ranking.

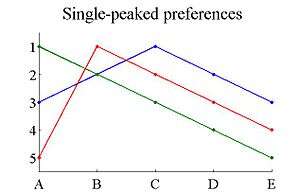
The ordering over the outcomes is A < B < C < D < E. The ideal outcome for the green agent is A, for the red it is B, for the blue it is C. For each agent, when we move away from his ideal outcome, the ranking decreases.

It can also be verified that, for each triplet of outcomes, one of them is never ranked last - the one in the middle. E.g., in {A,B,C}, B is never ranked last; in {C,D,E}, D is never ranked last; etc.

Non single-peaked preferences

If each of the two preferences represented by the following two graphs is added to the three preferences above, then the resulting group of four preferenes is not single-peaked:

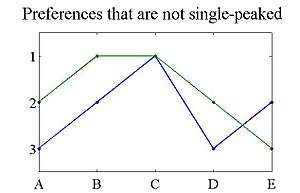
For the blue preferences, it can be seen that the preference ranking spikes down for "D" and then spikes up for "E". This proves that the blue preferences are not single-peaked with respect to the ordering A<B<C<D<E, but it still does not prove that there is no other ordering with which all four preferences are single-peaked. To formally prove this, consider the set of three outcomes {A, D, E}. Each of these outcomes is a worst outcome of some agent: A is worst for the red agent, D is worst for the blue agent, and E is worst for the green agent above. Therefore, no ordering on X can make the set of preferences single-peaked.

The green preferences are not formally single-peaked because they have two outcomes that are the most preferred: "B" and "C". Such preferences are sometimes called single-plateaued.

Interpretations

Single-peaked preferences have a number of interpretations for different applications.

A simple application of ideological preferences is to think of the outcome space ${\displaystyle \{x_{1},x_{2},\ldots ,x_{n}\}}$ as locations on a street and each ${\displaystyle x_{i}}$ as the address of an individual. Suppose a single bus stop has to be located on the street and every individual wishes to walk as little as possible to the stop. Individuals then have single-peaked preferences: individual ${\displaystyle i}$'s ideal point is ${\displaystyle x_{i}}$ and she dislikes other locations the farther they are to the west or the farther they are to the east.

The outcome space can also be thought as different policies in an ideological spectrum: policies from the Left vs policies from the Right; policies that are more liberal vs policies that are more conservative; policies that are pro free markets vs policies that are pro state intervention. Voters have single-peaked preferences if they have an ideal balance between the two directions of the ideological spectrum and if they dislike policies the farther away they are from their ideal point.

Single-dipped preferences

A group of agents is said to have single-dipped preferences over a set of possible outcomes if the outcomes can be ordered along a line such that:

1. Each agent has a "worst outcome" in the set, and -
2. For each agent, outcomes that are further from his worst outcome are preferred more.

See also

• Single-parameter mechanism

References

1. Black, Duncan (1948-02-01). "On the Rationale of Group Decision-making". Journal of Political Economy. 56 (1): 23–34. doi:10.1086/256633. ISSN 0022-3808.
2. Baumol, William J.; Arrow, Kenneth J. (1952-01-01). "Social Choice and Individual Values". Econometrica. 20 (1): 110. doi:10.2307/1907815. ISSN 0012-9682.
3. Ballester, Miguel A.; Haeringer, Guillaume (2010-07-15). "A characterization of the single-peaked domain". Social Choice and Welfare. 36 (2): 305–322. doi:10.1007/s00355-010-0476-3. ISSN 0176-1714.

• Austen-Smith, David & Jeffrey Banks (2000). Positive Political Theory I: Collective Preferences. University of Michigan Press. ISBN 978-0-472-08721-1.
• Mas-Colell, Andreu, Michael D. Whinston, and Jerry R. Green (1995). Microeconomic Theory. Oxford University Press. ISBN 978-0-19-507340-9.CS1 maint: multiple names: authors list (link)
• Moulin, Hervé (1991). Axioms of Cooperative Decision Making. Cambridge University Press. ISBN 978-0-521-42458-5.