Sim (pencil game)

Sim is a pencil-and-paper game that is played by two players.

The playing area

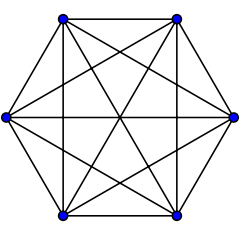
Gameplay

Six dots ('vertices') are drawn. Each dot is connected to every other dot by a line ('edge').

Two players take turns coloring any uncolored lines. One player colors in one color, and the other colors in another color, with each player trying to avoid the creation of a triangle made solely of their color (only triangles with the dots as corners count; intersections of lines are not relevant); the player who completes such a triangle loses immediately.

Analysis

Ramsey theory can also be used to show that no game of Sim can end in a tie. Specifically, since the Ramsey number R(3,3)=6, any two-coloring of the complete graph on 6 vertices (K6) must contain a monochromatic triangle, and therefore is not a tied position. This will also apply to any super-graph of K6. For another proof that there must eventually be a triangle of either color, see the Theorem on friends and strangers.

Computer search has verified that the second player can win Sim with perfect play, but finding a perfect strategy that humans can easily memorize is an open problem.

The game of Sim is one example of a Ramsey game. Other Ramsey games are possible. For instance, the players can be allowed to color more than one line during their turns. Another Ramsey game similar to Sim and related to Ramsey number R(4,4)=18, which again cannot end in a tie, is played on 18 vertices and the 153 edges between them. The two players must avoid to color a monochromatic tetrahedron (a three-dimensional pyramid with four triangular faces).

The Ramsey number R(3,3,3)=17 implies that any three-coloring of the complete graph on 17 vertices must contain a monochromatic triangle. A corresponding Ramsey game uses pencils of three colors. One approach can have three players compete, while another would allow two players to alternately select any of the three colors to paint an edge of the graph, until a player loses by completing a monochromatic triangle. Finding perfect winning strategies for these variants is most likely out of reach.

A technical report[1] by Wolfgang Slany is available online, with many references to literature on Sim, going back to the game's introduction by Gustavus Simmons in 1969,[2] including proofs and estimates of the difficulty as well as computational complexity of Sim and other Ramsey games.

Software

A self-improving Java applet including its source code is available[3] for online play against a computer program.

An app including its source code in the visual multi-platform Catrobat programming language is available[4] for playing it against one's smartphone.

gollark: Well, it has to be decryptable by payment terminals, so that's useless.
gollark: Anyway, pretty much the only secure way to do this magcard thing would be... having payment terminals bother a central server, and even that would have problems.
gollark: (that's probably a metaphor for life somehow)
gollark: I'm not sure tying your currency to Krist is a good idea. Krist has really weird wealth distribution because mining was fifty times more profitable before.
gollark: It probably works on OS caches anyway.

References
  1. Graph Ramsey Games by Wolfgang Slany at arXiv
  2. Simmons, Gustavus J. "The game of SIM," J. Recreational Mathematics, 2(2), 1969, pp. 66.
  3. Java applet page, including source code
  4. App for smartphones, including source code
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.