Shear force
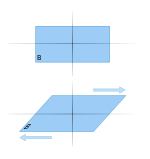
Shearing forces are unaligned forces pushing one part of a body in one specific direction, and another part of the body in the opposite direction. When the forces are aligned into each other, they are called compression forces. An example is a deck of cards being pushed one way on the top, and the other at the bottom, causing the cards to slide. Another example is when wind blows at the side of a peaked roof of a house - the side walls experience a force at their top pushing in the direction of the wind, and their bottom in the opposite direction, from the ground or foundation. William A. Nash defines shear force in terms of planes: "If a plane is passed through a body, a force acting along this plane is called a shear force or shearing force."[1]

Shear force of steel and bolts
Here follows a short example of how to work out the shear force of a piece of steel. The factor of 0.6 used to change from tensile to shear force could vary from 0.58–0.62 and will depend on application.
Steel called EN8 bright has a tensile strength of 800 MPa and mild steel has a tensile strength of 400 MPa.
To work out the force to shear a 25 mm diameter round steel EN8 bright;
- Area of the 25 mm round steel in mm2 = (12.52)(π) ≈ 490.8 mm2
- 0.8 kN/mm2 × 490.8 mm2 = 392.64 kN ≈ 40 tonne-force
- 40 tonne-force × 0.6 (to change force from tensile to shear) = 24 tonne-force
When working with a riveted or tensioned bolted joint, the strength comes from friction between the materials bolted together. Bolts are correctly torqued to maintain the friction. The shear force only becomes relevant when the bolts are not torqued.
A bolt with property class 12.9 has a tensile strength of 1200 MPa (1 MPa = 1 N/mm2) or 1.2 kN/mm2 and the yield strength is 0.90 times tensile strength, 1080 MPa in this case.
A bolt with property class 4.6 has a tensile strength of 400 MPa (1 MPa = 1 N/mm2) or 0.4 kN/mm2 and yield strength is 0.60 times tensile strength, 240 MPa in this case.
In case of fasteners, proof load is specified as it gives a real-life picture about the characteristics of the bolt.
See also
- ASTM F568M, shear force resistance
- Cantilever method
- Resal effect
- Newton's laws of motion § Newton's third law
References
- William A. Nash (1 July 1998). Schaum's Outline of Theory and Problems of Strength of Materials. McGraw-Hill Professional. p. 82. ISBN 978-0-07-046617-3. Retrieved 20 May 2012.