Shared Risk Resource Group

Shared risk resource group (commonly referred to as shared risk group or SRG) is a concept in optical mesh network routing that different networks may suffer from a common failure if they share a common risk or a common SRG. SRG is not limited to Optical mesh networks: SRGs are also used in MPLS, IP networks, and synchronous optical networks.

An SRG failure makes multiple circuits go down because of the failure of a common resource those networks share. There are three main shared risk groups:

  • Shared risk link group (SRLG)
  • Shared risk node group (SRNG)
  • Shared risk equipment group (SREG).

Failure recovery is a crucial in all types of networks. The MPLS as well as the IP network uses the high speed capabilities of modern optical networks. SRLGs typically deal with links between fiber optic nodes, but that is not always the case.[1][2] SRLG can also be modeled if the links contain transmission lines instead of fiber optic cable. SRG modeling is also used when a provider generates a service-level agreement with a client with various protection schemes.[3]

Types of SRRGs

SRLG
Example of SRLG

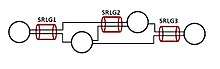
Fiber spans are fiber optic cables that connect two nodes. In practice, these cables are bundled on one concrete conduit or power/telephone pole (aerial), which creates a shared risk link Group. If, for example, if there is a cut on a fiber span, it takes down all circuits (upper layer logical links) that use that particular SRLG. The term SRLG may have first appeared in 2000.[4][5] Early work (from 1990s) that considered SRLG (before the term was coined) in understanding implications due to SRLG, and designing for survivability and restoration by considering SRLG can be found in [6] [7] .[8]

SRNG
Example of SRNG

In optical mesh networks, nodes are junctions of fiber spans. Some nodes might contain highly sophisticated routing equipment— while others may be just a patch panel. Whatever the case, a node is a shared risk node group—because if the node fails, the failure affects all signals through that particular node.

SREG

Shared risk group also extends within a node itself—in particular nodes that contain multi-port network cards. Dense wavelength division multiplexing equipment are also considered SREG because if a DWDM Mux fails that affects all of the channels through that DWDM. The same is true for multi-port network cards. When routing over SNRG is not possible, circuit-pack diversity with-in the same node can lessen the risk of failure.

Diverse Routing in SRG failure

Failure recovery is an essential part of any optical based network. When provisioning a circuit, engineers typically use a shortest path algorithm, such as Dijkstra. Calculations for a protection path must take into account that the protection path must provide 100% SRG protection. In other words, the protection path cannot go through the same SRLG or SRNG. If SRG diversity is not achieved then the failure of that SRG fails both primary path and back-up paths simultaneously. Therefore, the two calculated paths must be SRG diverse.[6][8][9]

There has been recent studies that have proved that the SRG diverse routing is in fact NP-complete.[10] There is currently no known discrete method to solve this real world problem for large-scale network. People have been able to solve this problem by finding a heuristic solution.[1]

NP Completeness
Graph used to prove NP-completeness of the SRG diverse problem

The SRG diverse routing problem has proven to be NP-complete. To prove something is NP-complete, it is sufficient to prove that the problem closely resembles another well-known NP-complete problem. To prove the case, engineers introduce a graph, as shown in the picture. The graph depicts that, between two nodes, there exist multiple paths, which may include other nodes. The parallel paths in sub-graphs (circled in blue) belong to the same SRLG.

Finding an SRG diverse path is the same as finding two disjoint subsets, such that each subset contains at least one common element. This is equivalent to the set-splitting problem, which has been proven NP-complete. Therefore, the SRG diverse routing problem is also NP-complete.[11] (SRLG is solvable using Suurballe's algorithm)

Graph Transformation Approach
The approach fails here because the algorithm would find a non-existent route

There has been many attempts to overcome the fact that there is no solution for the SRG diverse routing problem. One of these attempts is by means of a graph transformation approach.[9] This method takes the original network graph and applies some transformations to the graph to obtain a transformed graph that overcomes the SRG diverse problem to some degree. However, this method has its own shortcomings.

After obtaining the transformed graph one would simply compute the primary path using a known shortest path algorithm such as Dijkstra’s. On computing the primary path, and removing all nodes and links in that path, run the algorithm again on the remaining network. There may be instances when, due to topological restrictions, unavoidable traps could be introduced that prevent the algorithm from finding a solution. There are also avoidable traps, which come from parameter restrictions such as cost. These can be overcome by reconsidering the parameter values or altering the algorithm to make it more robust.

This method is limited, the following conditions must be met to calculate two SRG diverse paths:

  • The number of links to an SRLG must be lower than the degree of the node the SRLG is incident on
  • An SRLG cannot be a subset of another SRLG
  • An edge (two nodes connected by a link) can share two SRLGs at most

This approach works only in very narrow circumstances. When looking at actual large scale implemented networks this approach is useless because the links in the network greatly exceed these restrictions. A typical link can contain as many as 50,000 SRLG.[12] One of the reasons this approach falls short is in the case of two independent edges where links fall in the same SRLG, even though the algorithm might find a path that would be incorrect because there would be no physical route.[9]

Example of original topology of a network
The transformed graph
This graph meets the restriction 1 because the node 3 has a degree of 3 meanwhile it only has 2 incident SRLGs

SRLG Auto-discovery

Modern network providers have various ways to deal with shared risk group diverse routing.[13] SRGs are now closely linked to service level agreements. 100% SRG diverse is not possible in some cases. An example of this is the link that goes from the clients office to the providers local offices. Often, the primary path and the back-up path exit the building at the same point, which in itself is an SRG.

The most common way to deal with SRG is to keep a database of all the networks SRGs. The means of updating these databases are of great concern, because manual updating creates room for human error. It can also delay updating, because the network topology changes rapidly. Auto-discovery of SRGs has been proposed. SRG auto-discovery uses all components in the actual physical layer. Active components are those that can be monitored, and they include: amplifiers, transponders, regenerators, and DWDM Mux/DeMuxs. Passive components cannot be monitored electronically, and include conduits, simple patch-panels, and splice points.

Fitting these components with GPS would help identify component position to a SRLG management system. The system could then generate all of the SRLGs based on the information. This would also help localize the failure, which would further reduce down time of that failed SRG. A supervisory channel could connect to all active components to provide management and supervision.[14](registration required)

Because longer SRLGs have more components it is easier to detect them. Shorter SRLGs are harder to detect because they don’t have as many components as the longer SRLGs. The parameter that determines just how well SRLG can be detected is the amplifier spacing to the SRLG length. SRLG that span anything over 50 miles and over are nearly 100% detected.[15]

gollark: A Python interpreter exists on most modern systems which aren't bad like Windows, and there are tons of implementations.
gollark: SIMD™!
gollark: Well, I suppose you could tcc.
gollark: Retroactively erase knowledge of it, why?
gollark: You're forgetting the entire OS, gcc/clang, the entire x86 architecture, the particular implementation of x86 in your computer, and the various standards allowing this to interoperate nicely.

See also

Telecommunications and networking

Telecommunications equipment

Packet networking

Availability

References
  1. Dahai Xu; Guangzhi Li; Ramamurthy, Byrav; Chiu, Angela; Dongmei Wang; Doverspike, Robert. "SRLG-Diverse Routing of Multiple Circuits in a Heterogeneous OPM" (PDF). Retrieved 2012-12-15.
  2. Shao, X.; Bai, Y.; Cheng, X.; Yeo, Y. K.; Zhou, L.; Ngoh, L. H. (2011). "Best Effort SRLG Failure Protection for Optical WDM Networks". Journal of Optical Communications and Networking. 3 (9): 739. doi:10.1364/JOCN.3.000739.
  3. Lu Shen; Xi Yang; Ramamurthy, Byrav (2003). "Shared Risk Link Group (SRLG)-Diverse Path Provisioning under Hybrid Service Level Agreements". IEEE/ACM Transactions on Networking: 918–931. CiteSeerX 10.1.1.112.9508.
  4. Bala Rajagopalan; Debanjan Saha (2000). "Link Bundling Considerations in Optical Networks (Internet Draft)".
  5. Bala Rajagopalan; Dimitrios Pendarakis; Debanjan Saha; Ramu S. Ramamoorthy; Krishna Bala (September 2000). "IP over Optical Networks: Architectural Aspects". IEEE Communications Magazine. 38 (9): 94–102. CiteSeerX 10.1.1.24.7552. doi:10.1109/35.868148.
  6. Deep Medhi; Senthil Sankarappan (1993). "Impact of a Transmission Facility Link Failure on Dynamic Call Routing Circuit-Switched Networks under Various Circuit Layout Policies". Journal of Network and Systems Management. 1 (2): 143–169. doi:10.1007/BF01035885.
  7. Deep Medhi (1994). "A Unified Approach to Network Survivability for Teletraffic Networks: Models, Algorithms and Analysis". IEEE Transactions on Communications. 42 (2/3/4): 534–548. Bibcode:1994ITCom..42..534M. CiteSeerX 10.1.1.39.811. doi:10.1109/TCOMM.1994.577080.
  8. Deep Medhi; Rajeev Khurana (1995). "Optimization and Performance of Network Restoration Schemes for Wide-Area Teletraffic Networks". Journal of Network and Systems Management. 3 (3): 265–294. doi:10.1007/BF02138930.
  9. Datta, P.; Somani, A. K. (2008). "Graph transformation approaches for diverse routing in shared risk resource group (SRRG) failures". Computer Networks. 52 (12): 2381–2394. CiteSeerX 10.1.1.503.2290. doi:10.1016/j.comnet.2008.04.017.
  10. Proof of NP-completeness of the diverse routing problem with general SRGs (see section 7.1 in Appendix)
  11. Jian Qiang Hu (2003). "Diverse routing in optical mesh networks". IEEE Transactions on Communications. 51 (3): 489–494. doi:10.1109/TCOMM.2003.809779.
  12. "On shared risk link Group Optimization" (DOC). Research.att.com. Retrieved 2012-12-15. (from )
  13. Alicherry, Mansoor; Bhatia, Randeep; Saniee, Iraj; Sengupta, Sudipta. "SRLG Diversity Aware Protection Routing in Optical Mesh Networks" (PDF). Retrieved 2005-10-10.
  14. Sebos, P.; Yates, J.; Hjalmtysson, G.; Greenberg, A. (2001). "Auto-discovery of shared risk link groups". Auto-Discovery of SRGs. 3. Ieeexplore.ieee.org. pp. WDD3–W1–3. doi:10.1109/OFC.2001.928453. ISBN 978-1-55752-655-7.
  15. Sebos, Panagiotis; Yates, Jennifer; Rubenstein, Dan; Greenberg, Albert. "Effectiveness of SRG Auto-discovery in Optical Networks" (PDF). Retrieved 2012-12-15.

Further reading
  • "Path Routing in Mesh Optical Networks", by Eric Bouillet, Georgios Ellinas, Jean-Francois Labourdette, and Ramu Ramamurthy , ,
  • "Network Recovery: Protection and Restoration of Optical, SONET-SDH, IP, and MPLS", by Jean-Philippe Vasseur, Mario Pickavet, and Piet Demeester
  • "GMPLS Technologies: Broadband Backbone Networks and Systems" by Naoaki Yamanaka, Kohei Shiomoto, and EIJI AUTOR OKI
  • "Routing, Flow, and Capacity Design in Communication and Computer Networks", by M. Pióro and D. Medhi, Morgan Kaufmann Publishers (2004)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.