Separatrix (mathematics)
In mathematics, a separatrix is the boundary separating two modes of behaviour in a differential equation.[1]
Example
Consider the differential equation describing the motion of a simple pendulum:
where denotes the length of the pendulum, the gravitational acceleration and the angle between the pendulum and vertically downwards. In this system there is a conserved quantity H (the Hamiltonian), which is given by
With this defined, one can plot a curve of constant H in the phase space of system. The phase space is a graph with along the horizontal axis and on the vertical axis – see the thumbnail to the right. The type of resulting curve depends upon the value of H.
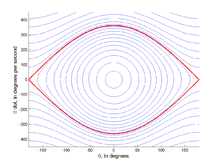
If then no curve exists (because must be imaginary).
If then the curve will be a simple closed curve which is nearly circular for small H and becomes "eye" shaped when H approaches the upper bound. These curves correspond to the pendulum swinging periodically from side to side.
If then the curve is open, and this corresponds to the pendulum forever swinging through complete circles.
In this system the separatrix is the curve that corresponds to . It separates — hence the name — the phase space into two distinct areas, each with a distinct type of motion. The region inside the separatrix has all those phase space curves which correspond to the pendulum oscillating back and forth, whereas the region outside the separatrix has all the phase space curves which correspond to the pendulum continuously turning through vertical planar circles.
References
- Blanchard, Paul, Differential Equations, 4th ed., 2012, Brooks/Cole, Boston, MA, pg. 469.
- Logan, J. David, Applied Mathematics, 3rd Ed., 2006, John Wiley and Sons, Hoboken, NJ, pg. 65.
External links
- Separatrix from MathWorld.