Schwarz lantern

In mathematics, the Schwarz lantern (also known as Schwarz's boot, after mathematician Hermann Schwarz) is a pathological example of the difficulty of defining the area of a smooth (curved) surface as the limit of the areas of polyhedra. The curved surface in question is a portion of a right circular cylinder. The discrete polyhedral approximation considered has ${\displaystyle 2n}$ axial "slices". ${\displaystyle 2m}$ vertices are placed radially along each slice at a circumferential distance of ${\displaystyle \pi /m}$ from each other. Importantly, the vertices are placed so they shift in phase by ${\displaystyle \pi /2m}$ with each slice.

Schwarz lantern with ${\displaystyle 2n=6}$ axial slices and ${\displaystyle 2m=10}$ radial vertices.

Hermann Schwarz showed in 1880 that it is not sufficient to simply increase ${\displaystyle m}$ and ${\displaystyle n}$ if we wish for the surface area of the polyhedron to converge to the surface area of the curved surface.[1] Depending on the relation of ${\displaystyle m}$ and ${\displaystyle n}$ the area of the lantern can converge to the area of the cylinder, to a limit arbitrarily larger than the area of the cylinder, to infinity or in other words to diverge. Thus, the Schwarz lantern demonstrates that simply connecting inscribed vertices is not enough to ensure surface area convergence.

Animation of Schwarz lantern convergence (or lack thereof) for various refinement strategies.

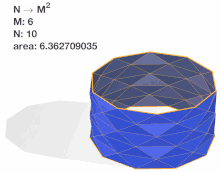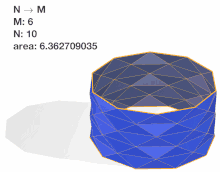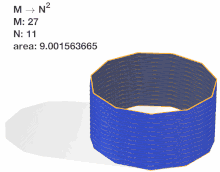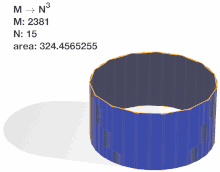
The polyhedral surface bears resemblance to a cylindrical paper lantern.

The sum of the angles at each vertex is equal to two flat angles (${\displaystyle 2\pi }$ radians). This has as a consequence that the Schwarz lantern can be folded out of a flat piece of paper.

Relation to arc length and surface area

In the work of Archimedes it already appears that the length of a circle can be approximated by the length of regular polyhedra inscribed or circumscribed in the circle. In general, for smooth or rectifiable curves their length can be defined as the supremum of the lengths of polygonal curves inscribed in them. The Schwarz lantern shows that surface area cannot be defined as the supremum of inscribed polyhedral surfaces.

History

Schwarz devised his construction as a counterexample to the erroneous definition in J. A. Serret's book Cours de calcul differentiel et integral, second volume, page 296 of the first edition or page 298 of the second edition, in which it is said:

Soit une portion de surface courbe terminee par un contour ${\displaystyle C}$; nous nommerons aire de cette surface la limite ${\displaystyle S}$ vers laquelle tend l'aire d'une surface polyedrale inscrite formee de faces triangulaires et terminee par un contour polygonal ${\displaystyle \Gamma }$ ayant pour limite le contour ${\displaystyle C}$.

Il faut demontrer que la limite ${\displaystyle S}$ existe et qu'elle est independante de la loi suivant laquelle decroissent les faces de la surface polyedrale inscrite'.

In English

Let a portion of curved surface end with a contour ${\displaystyle C}$; we will call the area of this surface the limit ${\displaystyle S}$ towards which the area of a polyhedron surface inscribed forms triangular faces and ends with a polygonal contour ${\displaystyle \Gamma }$ whose limit is the contour ${\displaystyle C}$.

It must be shown that the limit ${\displaystyle S}$ exists and that it is independent of the law according to which decreases the faces of the polyhedral surface inscribed.

Independently of Schwarz, Giuseppe Peano found the same counterexample while a student of his teacher Angelo Genocchi, who already knew about the difficulty on defining surface area from his communication with Schwarz. Genocchi informed Charles Hermite, who had been using Serret's erroneous definition in his course. After requesting details to Schwarz, Hermite revised his course and published the example in the second edition of his lecture notes (1883). The original note from Schwarz was not published until the second edition of his collected works in 1890.

Limits of the area

A straight circular cylinder of radius ${\displaystyle r}$ and height ${\displaystyle h}$ can be parametrized in Cartesian coordinates using the equations

${\displaystyle x=r\cos(u)}$

${\displaystyle y=r\sin(u)}$

${\displaystyle z=v}$

for ${\displaystyle 0\leq u\leq 2\pi }$ and ${\displaystyle 0\leq v\leq h}$. The Schwarz lantern is a polyhedron with ${\displaystyle 4mn}$ triangular faces inscribed in the cylinder.

The vertices of the polyhedron correspond in the parametrization to the points

${\displaystyle u={\frac {2\mu \pi }{m}}}$

${\displaystyle v={\frac {\nu h}{n}}}$

and the points

${\displaystyle u={\frac {(2\mu +1)\pi }{m}}}$

${\displaystyle v={\frac {(2\nu +1)h}{2n}}}$

with ${\displaystyle \mu =0,1,2,\ldots ,m-1}$ and ${\displaystyle \nu =0,1,2,\ldots ,n-1}$. All the faces are isosceles triangles congruent to each other. The base and the height of each of these triangles have lengths

${\displaystyle 2r\sin \left({\frac {\pi }{m}}\right){\text{ and }}{\sqrt {r^{2}\left[1-\cos \left({\frac {\pi }{m}}\right)\right]^{2}+\left({\frac {h}{2n}}\right)^{2}}}}$

respectively. This gives a total surface area for the Schwarz lantern

${\displaystyle S(m,n)=4mnr\sin \left({\frac {\pi }{m}}\right){\sqrt {4r^{2}\sin ^{4}\left({\frac {\pi }{2m}}\right)+\left({\frac {h}{2n}}\right)^{2}}}}$.

Simplifying sines when ${\displaystyle m\to \infty }$

${\displaystyle S(m,n)\simeq 4\pi nr{\sqrt {\left({\frac {\pi ^{2}r}{2m^{2}}}\right)^{2}+\left({\frac {h}{2n}}\right)^{2}}}=2\pi r{\sqrt {\left(\pi ^{2}r{\frac {n}{m^{2}}}\right)^{2}+h^{2}}}}$.

From this formula it follows that:

1. If ${\displaystyle n=am}$ for some constant ${\displaystyle a}$, then ${\displaystyle S(m,am)\to 2\pi rh}$ when ${\displaystyle m\to \infty }$. This limit is the surface area of the cylinder in which the Schwarz lantern is inscribed.
2. If ${\displaystyle n=am^{2}}$ for some constant ${\displaystyle a}$, then ${\displaystyle S(m,am^{2})\to 2\pi r{\sqrt {\pi ^{4}r^{2}a^{2}+h^{2}}}}$ when ${\displaystyle m\to \infty }$. This limit depends on the value of ${\displaystyle a}$ and can be made equal to any number not smaller than the area of the cylinder ${\displaystyle 2r\pi h}$.
3. If ${\displaystyle n=am^{3}}$, then ${\displaystyle S(m,am^{3})\to \infty }$ as ${\displaystyle m\to \infty }$.

Notes

1. M. Berger, Geometry I, Springer-Verlag, 1994, p. 263

References

• Schwarz, H. A. (1890). Gesammelte Mathematische Abhandlungen von H. A. Schwarz. Verlag von Julius Springer. pp. 309–311.CS1 maint: ref=harv (link)
• Dubrovsky, Vladimir (1991). "In search of a definition of surface area". Quantum. pp. 6-9 and 64.CS1 maint: ref=harv (link)

External links

• https://www.cut-the-knot.org/Outline/Calculus/SchwarzLantern.shtml
• Article in Schwarz collected works
• V. Dubrovsky's article.
• Frieda Zames' article.