Salamis Tablet

The Salamis Tablet is a marble counting board (an early counting device) dating from around 300 B.C. that was discovered on the island of Salamis in 1846. A precursor to the abacus, it is thought that it represents an ancient Greek means of performing mathematical calculations common in the ancient world. Pebbles (Latin: calculi) were placed at various locations and could be moved as calculations were performed. The marble tablet itself has dimensions of approximately 150 × 75 × 4.5 cm.[1]

An early photograph of the Salamis Tablet, 1899. The original is marble and is held by the National Museum of Epigraphy, in Athens.

Discovery

Originally thought to be a gaming board, the slab of white marble is currently at the Epigraphical Museum in Athens.

Description

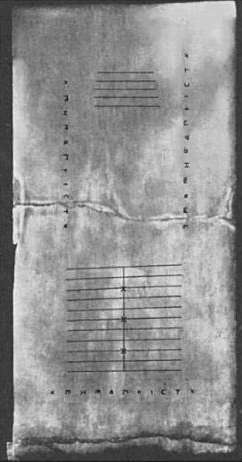
Five groups of markings appear on the tablet. The three sets of Greek symbols arranged along the left, right and bottom edges of the tablet are numbers from the acrophonic system. In the center of the tablet – a set of five parallel lines equally divided by a vertical line, capped with a semicircle at the intersection of the bottom-most horizontal line and the single vertical line. Below a wide horizontal crack is another group of eleven parallel lines. These are divided into two sections by a line perpendicular to them but with the semicircle at the top of the intersection; the third, sixth and ninth of these lines are marked with a cross where they intersect with the vertical line.

Numerical representations

As with an abacus, pebbles represent small numbers (generally between zero and four) and a system of lines serves to group them by powers of ten. A pebble between the lines represents half the value of a pebble on the line above it. So a pebble on the first line represents a 1; above the first line is a 5; second line is 10; above the second line is 50; etc.

The vertical line divides positive and negative portions of the Salamis Tablet. Pebbles on the right side of the vertical line represent positive digits and those on the left side of the line represent negative digits.

A complete number is composed of various pebbles on lines and spaces, both on the positive and negative sides. For example, the number 4 might be represented as a pebble above the right side of the first line plus a pebble on the left side of the first line; the pebble on the right side lies between the first and second lines so it counts as a +5, whereas the pebble on the left side of the first line represents a −1, so the two pebbles together represent +4. Likewise, the number 90 might be represented as a pebble on the right side of the third line plus a pebble on the left side of the second line. Note that this way of representing integers corresponds to the set-theoretic (or foundational) construction of the integers as ordered pairs of natural numbers. (Cf. balanced ternary.)

Calculations

On this board, physical markers (indicators) were placed on the various rows or columns that represented different values. The indicators were not physically attached to the board.

On the tablet Greek numbers are represented. Already in the Ionian time period number systems were responsible for the written use, which became necessary because of the expanding commercial activity.

Two different number systems were developed, the older Attic or Herodian number system and the younger, Milesian system.

The two number systems differed in their use: the Attic predominantly served the commercial life for the adjustment of funds and goods data as well as for the designation of the columns on the abacus. For written calculations the Attic numeral system was unsuitable. The Milesian number system, with which one likewise assigned numbers to letters of the alphabet, was better suited for scientific mathematics. For example, Archimedes and Diophantus used the Milesian system.

The Greek writer Herodotus (485–425 BC) reports in his travels through Egypt that the Egyptians calculated from right to left, contrary to the Greek custom of left to right.[2] This may refer to moving pebbles on the counting board.[3]


gollark: I disagree strongly with this.
gollark: Denied. Initiating emergency η converter.
gollark: Topologically autoroute yourself UTTERLY, heavpoot.
gollark: It can't\* be that\*\* hard.
gollark: Thus, make metaesolang which does timing?

References
  1. The Abacus: A Brief History
  2. Herodotus 2.36
  3. Lang, Mabel. "Herodotos and the Abacus". Hesperia: The Journal of the American School of Classical Studies at Athens. 26 (3): 271. JSTOR 147100.

Further reading
  • Bradshaw, Gillian (2000), The Sand-Reckoner, Forge, ISBN 0312875819
  • Stephenson, Stephen Kent (July 2013), Ancient Computers, Part I - Rediscovery (2 ed.), ISBN 1490964371
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.