Rotating wall technique
The Rotating wall technique (or RW technique) is a method used to compress a single-component plasma (a cold dense gas of charged particles) confined in an electromagnetic trap. It is one of many scientific and technological applications that rely on storing charged particles in vacuum. This technique has found extensive use in improving the quality of these traps and in tailoring of both positron and antiproton (i.e. antiparticle) plasmas for a variety of end uses.
Overview
Single-component plasmas (SCP), which are a type of are a type of nonneutral plasma, have many uses, including studying a variety of plasma physics phenomena [1] and for the accumulation, storage and delivery of antiparticles. Applications include the creation and study of antihydrogen,[2][3][4] beams to study the interaction of positrons with ordinary matter and to create dense gases of positronium (Ps) atoms,[5][6][7] and the creation of Ps-atom beams.[8][9] The “rotating wall (RW) technique” uses rotating electric fields to compress SCP in PM traps radially to increase the plasma density and/or to counteract the tendency of plasma to diffuse radially out of the trap. It has proven crucial in improving the quality and hence utility of trapped plasmas and trap-based beams.
Principles of operation
For this application, a plasma is stored in a Penning–Malmberg (PM) trap[1] in a uniform magnetic field, B. The charge cloud is typically cylindrical in shape with dimension along B large compared to the radius. This charge produces a radial electric field which would tend to push the plasma outward. To counteract this, the plasma spins about the axis of symmetry producing a Lorentz force to balance that due to the electric field, and the plasma takes the form of a spinning charged rod. Such cold, single-component plasmas in PM traps can come to thermal equilibrium and rotate as a rigid body at frequency
where n is the plasma density.[10] As illustrated in Fig. 1, the RW technique uses an azimuthally segmented cylindrical electrode covering a portion of a plasma. Phased, sinusoidal voltages at frequency fRW are applied to the segments. The result is a rotating electric field perpendicular to the axis of symmetry of the plasma. This field induces an electric dipole moment in the plasma and hence a torque. Rotation of the field in the direction of, and faster than the natural rotation of the plasma acts to spin the plasma faster, thereby increasing the Lorentz force and producing plasma compression (cf. Figs. 2 and 3).[11]
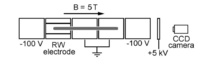
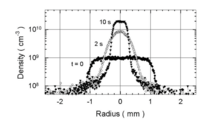
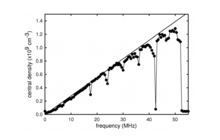
An important requirement for plasma compression using the RW technique is good coupling between the plasma and the rotating field. This is necessary to overcome asymmetry-induced transport which acts as a drag on the plasma and tends to oppose the RW torque. For high quality PM traps with little asymmetry induced transport, one can access a so-called “strong drive regime."[11][12] In this case, application of a rotating electric field at frequency results in the plasma spinning up to the applied frequency, namely fE = fRW (cf. Fig. 3). This has proven enormously useful as a way to fix plasma density simply by adjusting fRW.
History
The RW technique was first developed by Huang et al., to compress a magnetized Mg+ plasma.[13] The technique was soon thereafter applied to electron plasmas, where a segmented electrode, such as that described above, was used to couple to waves (Trivelpiece-Gould modes) in the plasma.[14] The technique was also used to phase-lock the rotation frequency of laser cooled single-component ion crystals.[15] The first use of the RW technique for antimatter was done using small positron plasmas without coupling to modes.[16] The strong drive regime, which was discovered somewhat later using electron plasmas,[17] has proven to be more useful in that tuning to (and tracking) plasma modes is unnecessary. A related technique has been developed to compress single-component charged gases in PM traps (i.e., charge clouds not in the plasma regime).[18][19]
Uses
The RW technique has found extensive use in manipulating antiparticles in Penning–Malmberg traps. One important application is the creation of specially tailored antiparticle beams for atomic physics experiments.[5] Frequently one would like a beam with a large current density. In this case, one compresses the plasma with the RW technique before delivery. This has been crucial in experiments to study dense gases of positronium (Ps) atoms and formation of the Ps2 molecule (e+e−e+e−) [5-7]. It has also been important in the creation of high-quality Ps-atom beams.[8][9]
The RW technique is used in three ways in the creation of low-energy antihydrogen atoms. Antiprotons are compressed radially by sympathetic compression with electrons co-loaded in the trap. The technique has also been used to fix the positron density before the positrons and antiprotons are combined.[2][3] Recently it was discovered that one could set all of the important parameters of the electron and positron plasmas for antihydrogen production using the RW to fix the plasma density and evaporative cooling to cool the plasma and fix the on-axis space charge potential. The result was greatly increased reproducibility for antihydrogen production.[4] In particular, this technique, dubbed SDREVC (strong drive regime evaporative cooling),[20] was successful to the extent that it increased the number of trappable antihydrogen by an order of magnitude. This is particularly important in that, while copious amounts of antihydrogen can be produced, the vast majority are at high temperature and cannot be trapped in the small well depth of the minimum-magnetic field atom traps.[21]
See also
- Positron
- Antiproton
- Penning trap
- Non-neutral plasmas
- Annihilation
- Positronium
- Antihydrogen
References
- Dubin, Daniel H. E.; O’Neil, T. M. (1999-01-01). "Trapped nonneutral plasmas, liquids, and crystals (the thermal equilibrium states)". Reviews of Modern Physics. American Physical Society (APS). 71 (1): 87–172. doi:10.1103/revmodphys.71.87. ISSN 0034-6861.
- Amoretti, M.; Amsler, C.; Bonomi, G.; Bouchta, A.; Bowe, P.; et al. (2002-09-18). "Production and detection of cold antihydrogen atoms". Nature. Springer Nature. 419 (6906): 456–459. doi:10.1038/nature01096. ISSN 0028-0836.
- Gabrielse, G.; Bowden, N. S.; Oxley, P.; Speck, A.; Storry, C. H.; et al. (2002-10-31). "Background-Free Observation of Cold Antihydrogen with Field-Ionization Analysis of Its States". Physical Review Letters. American Physical Society (APS). 89 (21): 213401–213404. doi:10.1103/physrevlett.89.213401. ISSN 0031-9007.
- Ahmadi, M.; Alves, B. X. R.; Baker, C. J.; Bertsche, W.; Capra, A.; et al. (2018-04-04). "Characterization of the 1S–2S transition in antihydrogen". Nature. Springer Science and Business Media LLC. 557 (7703): 71–75. doi:10.1038/s41586-018-0017-2. ISSN 0028-0836.
- Danielson, J. R.; Dubin, D. H. E.; Greaves, R. G.; Surko, C. M. (2015-03-17). "Plasma and trap-based techniques for science with positrons". Reviews of Modern Physics. American Physical Society (APS). 87 (1): 247–306. doi:10.1103/revmodphys.87.247. ISSN 0034-6861.
- Cassidy, D. B.; Mills, A. P. (2007). "The production of molecular positronium". Nature. Springer Science and Business Media LLC. 449 (7159): 195–197. doi:10.1038/nature06094. ISSN 0028-0836.
- Cassidy, D. B.; Hisakado, T. H.; Tom, H. W. K.; Mills, A. P. (2012-03-30). "Optical Spectroscopy of Molecular Positronium". Physical Review Letters. American Physical Society (APS). 108 (13): 133402–133405. doi:10.1103/physrevlett.108.133402. ISSN 0031-9007.
- Jones, A. C. L.; Moxom, J.; Rutbeck-Goldman, H. J.; Osorno, K. A.; Cecchini, G. G.; et al. (2017-08-02). "Focusing of a Rydberg Positronium Beam with an Ellipsoidal Electrostatic Mirror". Physical Review Letters. American Physical Society (APS). 119 (5): 053201. doi:10.1103/physrevlett.119.053201. ISSN 0031-9007.
- Michishio, K.; Chiari, L.; Tanaka, F.; Oshima, N.; Nagashima, Y. (2019). "A high-quality and energy-tunable positronium beam system employing a trap-based positron beam". Review of Scientific Instruments. AIP Publishing. 90 (2): 023305. doi:10.1063/1.5060619. ISSN 0034-6748.
- O’Neil, T. M.; Driscoll, C. F. (1979). "Transport to thermal equilibrium of a pure electron plasma". Physics of Fluids. AIP Publishing. 22 (2): 266–277. doi:10.1063/1.862577. ISSN 0031-9171.
- Danielson, J. R.; Surko, C. M. (2005-01-24). "Torque-Balanced High-Density Steady States of Single-Component Plasmas". Physical Review Letters. American Physical Society (APS). 94 (3): 035001–035004. doi:10.1103/physrevlett.94.035001. ISSN 0031-9007.
- Danielson, J. R.; Surko, C. M.; O’Neil, T. M. (2007-09-28). "High-Density Fixed Point for Radially Compressed Single-Component Plasmas". Physical Review Letters. American Physical Society (APS). 99 (13): 135005. doi:10.1103/physrevlett.99.135005. ISSN 0031-9007.
- Huang, X.-P.; Anderegg, F.; Hollmann, E. M.; Driscoll, C. F.; O'Neil, T. M. (1997). "Steady-State Confinement of Non-neutral Plasmas by Rotating Electric Fields". Physical Review Letters. 78 (5): 875–878. Bibcode:1997PhRvL..78..875H. doi:10.1103/PhysRevLett.78.875.
- F. Anderegg, E. M. Hollmann, and C. F. Driscoll, Rotating Field Confinement of Pure Electron Plasmas Using Trivelpiece-Gould Modes, Phys. Rev. Lett. 81, 4875-4878 (1998).
- X. P. Huang, J. J. Bollinger, T. B. Mitchell, and W. M. Itano, Phase-Locked Rotation of Crystallized Non-Neutral Plasmas by Rotating Electric Fields, Phys. Rev. Lett. 80, 73-76 (1998).
- R. G. Greaves and C. M. Surko, Radial Compression and Inward Transport of Positron Plasmas Using a Rotating Electric Field, Phys. Plasmas 8, 1879-1885 (2001).
- J. R. Danielson and C. M. Surko, Radial Compression and Torque-Balanced Steady States of Single-Component Plasmas in Penning–Malmberg Traps, Phys. Plasmas 13, 055706-055710 (2006).
- R. G. Greaves and J. M. Moxom, Compression of Trapped Positrons in a Single Particle Regime by a Rotating Electric Field, Phys. Plasmas 15, 072304 (2008).
- C. A. Isaac, C. J. Baker, T. Mortensen, D. P. v. d. Werf, and M. Charlton, Compression of Positron Clouds in the Independent Particle Regime Phys. Rev. Lett. 107, 033201-033204 (2011).
- M. Ahmadi, B. X. R. Alves, C. J. Baker, W. Bertsche, A. Capra, C. Carruth, et al., Enhanced Control and Reproducibility of Non-Neutral Plasmas, Phys. Rev. Lett. 120, 025001 (2018).
- C. Amole, M. D. Ashkezari, M. Baquero-Ruiz, W. Bertsche, P. D. Bowe, E. Butler, et al., Resonant Quantum Transitions in Trapped Antihydrogen Atoms, Nature 483, 439-444 (2012).