Road curve

Road curves are irregular bends in roads to bring a graduation change of direction. Similar curves are on railways and canals.

Curves provided in the horizontal plane are known as horizontal curves and are generally circular or parabolic. Curves provided in the vertical plane are known as vertical curve.

Five types of horizontal curves on roads and railways:

  • Simple curve
  • Compound curve
  • Opposite or serpentine curve
  • Deviation curve

Two types of vertical curves on roads:

  • Valley curve
  • Summit curve

Horizontal Curve

Simple curve
Diagram of simple curve

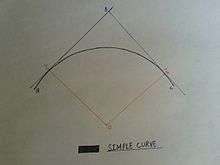
A simple curve has the same radius throughout and is a single arc of a circle, with two tangents meeting at the intersection (B in this diagram).

Compound curve
Diagram of compound curve

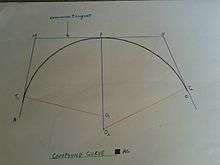
A compound curve has two or more simple curves with different radii that bend the same way and are on the same side of a common tangent. In this diagram, MN is the common tangent.

Reverse curve
Main article: Reverse curve
Diagram of reverse curve

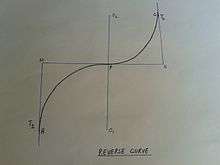
Also called a serpentine curve, it is the reverse of a compound curve, and two simple curves bent in opposite directions are on opposite sides of the common tangent.

Deviation curve
Diagram of deviation curve

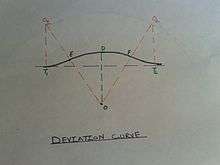
A deviation curve is simply a combination of two reverse curves. It is used when it is necessary to deviate from a given straight path to avoid intervening obstructions such as a building, a body of water, or other significant site.

Transition curve

Is a curve with a gradual change in elevation on the outside of the curve to help drivers comfortably take turns at faster speeds

Vertical road

Valley curve

Also called a sag curve, this curve dips down and then rises back up. These are placed in the base of hills. The opposite of summit curve.

Summit curve

Also called the crest curve, this cure rises and then dips down. At the peak of hills. The opposite of valley curve.

gollark: Eventually, if I commit to not responding to these threats, and it's sufficiently credible, people won't threaten me, probably!
gollark: No.
gollark: Besides, if I actually responded to this sort of threat, it would just incentivize people to keep threatening me.
gollark: Why?
gollark: Please remain socially distanced and do not attempt consumption of parents in crowded settings.

See also

References
    • Kobryń, Andrzej (2017), "Sample Applications of Transition Curves in Vertical Alignment", Transition Curves for Highway Geometric Design, Springer International Publishing, pp. 109–131, doi:10.1007/978-3-319-53727-6_9, ISBN 9783319537269


    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.