Repeating circle

Developed from the reflecting circle, the repeating circle is an instrument for geodetic surveying, invented by Etienne Lenoir in 1784,[1] while an assistant of Jean-Charles de Borda, who later improved the instrument. It was notable as being the equal of the great theodolite created by the renowned instrument maker, Jesse Ramsden. It was used to measure the meridian arc from Dunkirk to Barcelona by Jean Baptiste Delambre and Pierre Méchain.

12-inch repeating circle.
Borda reflecting circle, on display at Conservatoire national des arts et métiers.

Construction and operation

The repeating circle is made of two telescopes mounted on a shared axis with scales to measure the angle between the two. The instrument combines multiple measurements to increase accuracy with the following procedure:

Mode of operation:
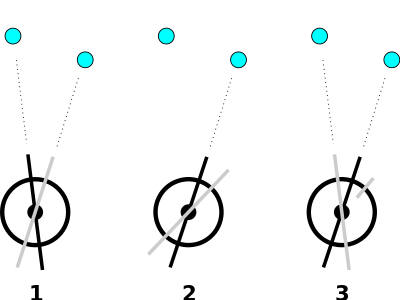
(1) The instrument is aligned so its plane includes the two points to be measured, and each telescope is aimed at a point;
(2) Keeping the angle between the telescopes locked, the left (black) telescope is rotated clockwise to aim at the right point;
(3) the right (gray) telescope's position is noted, and it is rotated back to the left point.

At this stage, the angle on the instrument is double the angle of interest between the points. Repeating the procedure causes the instrument to show 4× the angle of interest, with further iterations increasing it to 6×, 8×, and so on. In this way, many measurements can be added together, allowing some of the random measurement errors to cancel out.[2]

gollark: Of course somebody made `icosahedron.website`.
gollark: "I will join a technically interesting social network which nobody uses so I can talk to nobody."
gollark: It sounds like a very hydraz sort of thing to do.
gollark: I was looking at running an instance, but didn't bother to.
gollark: I'll find it when I'm at my computer, but there's a decent one used by the switchcraft ROM (but modified for os.loadAPI for some insane reason) and potatOS.

See also
  • Reflecting circles
  • Meridional definition
  • Grade (angle)

References
  1. Daumas, Maurice (1989). Scientific Instruments of the Seventeenth and Eighteenth Centuries and Their Makers. London: Portman Books. ISBN 978-0-7134-0727-3.
  2. Alder, Ken (2002). The Measure Of All Things. ISBN 0-7432-1675-X.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.