Region connection calculus

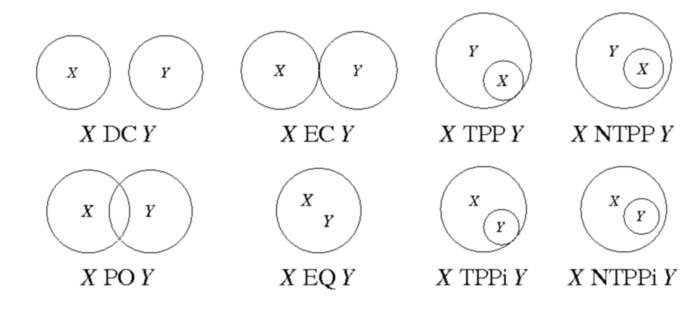
The region connection calculus (RCC) is intended to serve for qualitative spatial representation and reasoning. RCC abstractly describes regions (in Euclidean space, or in a topological space) by their possible relations to each other. RCC8 consists of 8 basic relations that are possible between two regions:

  • disconnected (DC)
  • externally connected (EC)
  • equal (EQ)
  • partially overlapping (PO)
  • tangential proper part (TPP)
  • tangential proper part inverse (TPPi)
  • non-tangential proper part (NTPP)
  • non-tangential proper part inverse (NTPPi)

From these basic relations, combinations can be built. For example, proper part (PP) is the union of TPP and NTPP.

Axioms

RCC is governed by two axioms.[1]

  • for any region x, x connects with itself
  • for any region x, y, if x connects with y, y will connects with x

Remark on the axioms

The two axioms describe two features of the connection relation, but not the characteristic feature of the connect relation.[2] For example, we can say that an object is less than 10 meters away from itself and that if object A is less than 10 meters away from object B, object B will be less than 10 meters away from object A. So, the relation 'less-than-10-meters' also satisfies the above two axioms, but does not talk about the connection relation in the intended sense of RCC.

Composition table

The composition table of RCC8 are as follows:

o DCECPOTPPNTPPTPPiNTPPiEQ
DC *DC,EC,PO,TPP,NTPPDC,EC,PO,TPP,NTPPDC,EC,PO,TPP,NTPPDC,EC,PO,TPP,NTPPDCDCDC
EC DC,EC,PO,TPPi,NTPPiDC,EC,PO,TPP,TPPi,EQDC,EC,PO,TPP,NTPPEC,PO,TPP,NTPPPO,TPP,NTPPDC,ECDCEC
PO DC,EC,PO,TPPi,NTPPiDC,EC,PO,TPPi,NTPPi*PO,TPP,NTPPPO,TPP,NTPPDC,EC,PO,TPPi,NTPPiDC,EC,PO,TPPi,NTPPiPO
TPP DCDC,ECDC,EC,PO,TPP,NTPPTPP,NTPPNTPPDC,EC,PO,TPP,TPPi,EQDC,EC,PO,TPPi,NTPPiTPP
NTPP DCDCDC,EC,PO,TPP,NTPPNTPPNTPPDC,EC,PO,TPP,NTPP*NTPP
TPPi DC,EC,PO,TPPi,NTPPiEC,PO,TPPi,NTPPiPO,TPPi,NTPPiPO,TPP,TPPi,EQPO,TPP,NTPPTPPi,NTPPiNTPPiTPPi
NTPPi DC,EC,PO,TPPi,NTPPiPO,TPPi,NTPPiPO,TPPi,NTPPiPO,TPPi,NTPPiPO,TPP,NTPP,TPPi,NTPPi,EQNTPPiNTPPiNTPPi
EQ DCECPOTPPNTPPTPPiNTPPiEQ
  • "*" denotes the universal relation.

Examples

The RCC8 calculus is intended for reasoning about spatial configurations. Consider the following example: two houses are connected via a road. Each house is located on an own property. The first house possibly touches the boundary of the property; the second one surely does not. What can we infer about the relation of the second property to the road?

The spatial configuration can be formalized in RCC8 as the following constraint network:

house1 DC house2
house1 {TPP, NTPP} property1
house1 {DC, EC} property2
house1 EC road
house2 { DC, EC } property1
house2 NTPP property2
house2 EC road
property1 { DC, EC } property2
road { DC, EC, TPP, TPPi, PO, EQ, NTPP, NTPPi } property1
road { DC, EC, TPP, TPPi, PO, EQ, NTPP, NTPPi } property2

Using the RCC8 composition table and the path-consistency algorithm, we can refine the network in the following way:

road { PO, EC } property1
road { PO, TPP } property2

That is, the road either overlaps with the second property, or is even (tangential) part of it.

Other versions of the region connection calculus include RCC5 (with only five basic relations - the distinction whether two regions touch each other are ignored) and RCC23 (which allows reasoning about convexity).

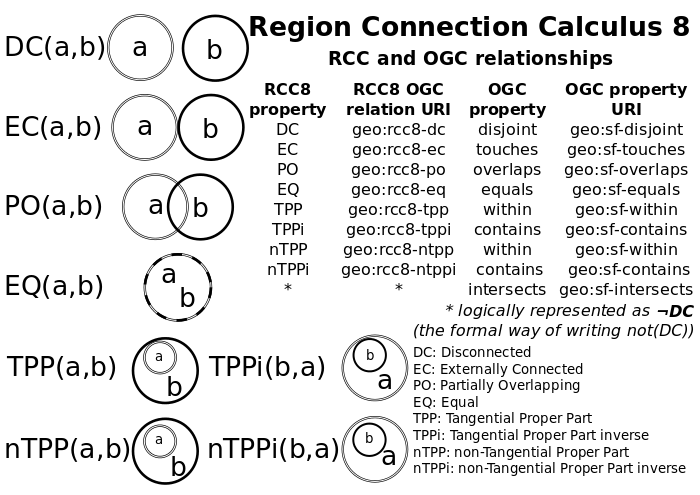
RCC8 use in GeoSPARQL

RCC8 has been partially implemented in GeoSPARQL as described below:

A graphical representation of Region Connection Calculus (RCC: Randell, Cui and Cohn, 1992) and the links to the equivalent naming by the Open Geospatial Consortium (OGC) with their equivalent URIs.

Implementations
  • GQR is a reasoner for RCC-5, RCC-8, and RCC-23 (as well as other calculi for spatial and temporal reasoning)
gollark: Well, thanks to AMD being less evil, on Linux the drivers are just built into the kernel or something and work with basically no hassle.
gollark: Nvidia's drivers are worse. They try and push you into this "GeForce Experience" thing or something, work poorly on Linux, and deliberately don't work in VMs because Nvidia is Nvidia.
gollark: Better in what way?
gollark: nvidia bad because artificial market segmentation through drivers, poor linux support, and high pricing
gollark: > not running an adblocker at all times

References
  1. Randell et. al. 1992
  2. Dong 2008
  • Randell, D.A.; Cui, Z; Cohn, A.G. (1992). "A spatial logic based on regions and connection". 3rd Int. Conf. on Knowledge Representation and Reasoning. Morgan Kaufmann. pp. 165–176.
  • Anthony G. Cohn; Brandon Bennett; John Gooday; Micholas Mark Gotts (1997). "Qualitative Spatial Representation and Reasoning with the Region Connection Calculus". GeoInformatica. 1 (3): 275–316. doi:10.1023/A:1009712514511..
  • Renz, J. (2002). Qualitative Spatial Reasoning with Topological Information. Lecture Notes in Computer Science. 2293. Springer Verlag. doi:10.1007/3-540-70736-0. ISBN 978-3-540-43346-0.
  • Dong, Tiansi (2008). "A Comment on RCC: From RCC to RCC⁺⁺". Journal of Philosophical Logic. 34 (2): 319–352. doi:10.1007/s10992-007-9074-y. JSTOR 41217909..

See also
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.