Rectilinear Steiner tree

The rectilinear Steiner tree problem, minimum rectilinear Steiner tree problem (MRST), or rectilinear Steiner minimum tree problem (RSMT) is a variant of the geometric Steiner tree problem in the plane, in which the Euclidean distance is replaced with the rectilinear distance. The problem may be formally stated as follows: given n points in the plane, it is required to interconnect them all by a shortest network which consists only of vertical and horizontal line segments. It can be shown that such a network is a tree whose vertices are the input points plus some extra points (Steiner points).[1]

The problem arises in the physical design of electronic design automation. In VLSI circuits, wire routing is carried out by wires running only in vertical and horizontal directions, due to high computational complexity of the task. Therefore wire length is the sum of the lengths of vertical and horizontal segments, and the distance between two pins of a net is actually the rectilinear distance ("Manhattan distance") between the corresponding geometric points in the design plane.[1]

Properties
Hanan grid for a 5-vertex case

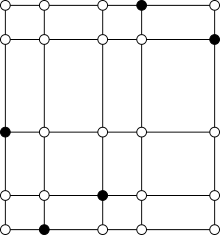
It is known that the search for the RSMT may be restricted to the Hanan grid, constructed by drawing vertical and horizontal lines through each vertex.[2]

Computational complexity

The RSMT is an NP-hard problem, and as with other NP-hard problems, common approaches to tackle it are approximate algorithms, heuristic algorithms, and separation of efficiently solvable special cases. An overview of the approaches to the problem may be found in the 1992 book by Hwang, Richards and Winter, The Steiner Tree Problem.[3]

Special cases

Single-trunk Steiner trees
A MSTST

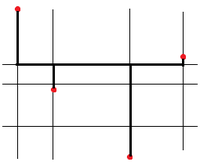
The single-trunk Steiner tree is a tree that consists of a single horizontal segment and some vertical segments. A minimum single-trunk Steiner tree problem (MSTST) may be found in linear time.

The idea is that STSTs for a given point set essentially have only one "degree of freedom", which is the position of the horizontal trunk. Further, it easy to see that if the Y-axis is split into segments by Y-coordinates of input points, then the length of a STST is constant within any such segment. Finally, it will be minimal if the trunk has the closest possible numbers of points below and above it. Therefore an optimal position of the trunk are defined by a median of the set of Y-coordinates of the points, which may be found in linear time. Once the trunk is found, the vertical segments may be easily computed. Notice however that while the construction of the connecting net takes linear time, the construction of the tree which involves both input points and Steiner points as its vertices will require O(n log n) time, since it essentially accomplishes sorting of the X-coordinates of the input points (along the split of the trunk into the edges of the tree).[4]

A MSTST is fast to compute but is a poor approximation of the MRST. A better approximation, called the refined single trunk tree, may be found in O(n log n) time. It is optimal for point sets of sizes up to 4.[5]

Approximations and heuristics

A number of algorithms exist which start from the rectilinear minimum spanning tree (RMST; the minimum spanning tree in the plane with rectilinear distance) and try to decrease its length by introducing Steiner points. The RMST itself may be up to 1.5 times longer than MRST.[6]

gollark: For another thing, as I found out while reading a complaint by mathematicians about the use of Riemann integrals over gauge integrals, if you always take the point to "sample" as the left/right/center of each partition *and* the thing is evenly divided up into partitions, it's actually wrong in some circumstances.
gollark: For one thing, the sum operator is very bee there because it does not appear to be counting integers.
gollark: It's wrong and abuse-of-notationy however.
gollark: And this isn't even *used anywhere* except that one or two of the integration questions use this as an extra layer of indirection.
gollark: The sum there makes no sense, and I'm pretty sure this is actually wrong for some integrals.

References
  1. Naveed Sherwani, "Algorithms for VLSI Physical Design Automation"
  2. M. Hanan, On Steiner’s problem with rectilinear distance, J. SIAM Appl. Math. 14 (1966), 255 - 265.
  3. F.K. Hwang, D.S. Richards, P. Winter, The Steiner Tree Problem. Elsevier, North-Holland, 1992, ISBN 0-444-89098-X (hardbound) (Annals of Discrete Mathematics, vol. 53).
  4. J. Soukup. "Circuit Layout". Proceedings of the IEEE, 69:1281–1304, October 1981
  5. H. Chen, C. Qiao, F. Zhou, and C.-K. Cheng. "Refined single trunk tree: A rectilinear Steiner tree generator for interconnect prediction". In: Proc. ACM Intl. Workshop on System Level Interconnect Prediction, 2002, pp.85–89.
  6. F. K. Hwang. "On Steiner minimal trees with rectilinear distance." SIAM Journal on Applied Mathematics, 30:104–114, 1976.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.