Rectified 24-cell honeycomb
In four-dimensional Euclidean geometry, the rectified 24-cell honeycomb is a uniform space-filling honeycomb. It is constructed by a rectification of the regular 24-cell honeycomb, containing tesseract and rectified 24-cell cells.
| Rectified 24-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | r{3,4,3,3} rr{3,3,4,3} r2r{4,3,3,4} r2r{4,3,31,1} |
| Coxeter-Dynkin diagrams |
|
| 4-face type | Tesseract Rectified 24-cell |
| Cell type | Cube Cuboctahedron |
| Face type | Square Triangle |
| Vertex figure |  Tetrahedral prism |
| Coxeter groups | , [3,4,3,3] , [4,3,3,4] , [4,3,31,1] , [31,1,1,1] |
| Properties | Vertex transitive |
Alternate names
- Rectified icositetrachoric tetracomb
- Rectified icositetrachoric honeycomb
- Cantellated 16-cell honeycomb
- Bicantellated tesseractic honeycomb
Symmetry constructions
There are five different symmetry constructions of this tessellation. Each symmetry can be represented by different arrangements of colored rectified 24-cell and tesseract facets. The tetrahedral prism vertex figure contains 4 rectified 24-cells capped by two opposite tesseracts.
| Coxeter group | Coxeter diagram |
Facets | Vertex figure | Vertex figure symmetry (order) |
|---|---|---|---|---|
= [3,4,3,3] |
4: 1: |
 |
(48) | |
| 3: 1: 1: |
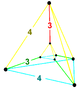 |
(12) | ||
= [4,3,3,4] |
2,2: 1: |
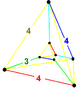 |
(8) | |
= [31,1,3,4] |
1,1: 2: 1: |
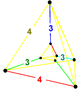 |
(4) | |
= [31,1,1,1] |
1,1,1,1: 1: |
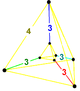 |
(2) |
gollark: Some elliptic curve lib.
gollark: I don't have GPG™ for CC.
gollark: Nope!
gollark: However, you *could* host actual potatOS files, they can be signed now.
gollark: I don't trust you enough to host potatOS command.
See also
Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- 16-cell honeycomb
- 24-cell honeycomb
- Truncated 24-cell honeycomb
- Snub 24-cell honeycomb
- 5-cell honeycomb
- Truncated 5-cell honeycomb
- Omnitruncated 5-cell honeycomb
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs) Model 93
- Klitzing, Richard. "4D Euclidean tesselations"., o3o3o4x3o, o4x3o3x4o - ricot - O93
Fundamental convex regular and uniform honeycombs in dimensions 2-9 | ||||||
|---|---|---|---|---|---|---|
| Space | Family | / / | ||||
| E2 | Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| En-1 | Uniform (n-1)-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.