Rectangular mask short-time Fourier transform

In mathematics, a rectangular mask short-time Fourier transform has the simple form of short-time Fourier transform. Other types of the STFT may require more computation time than the rec-STFT. Define its mask function

${\displaystyle w(t)={\begin{cases}\ 1;&|t|\leq B\\\ 0;&|t|>B\end{cases}}}$

B = 50, x-axis (sec)

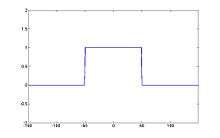
We can change B for different signal.

Rec-STFT

${\displaystyle X(t,f)=\int _{t-B}^{t+B}x(\tau )e^{-j2\pi f\tau }\,d\tau }$

Inverse form

${\displaystyle x(t)=\int _{-\infty }^{\infty }X(t_{1},f)e^{j2\pi ft}\,df{\text{ where }}t-B<t_{1}<t+B}$

Property

Rec-STFT has similar properties with Fourier transform

• Integration

(a)

${\displaystyle \int _{-\infty }^{\infty }X(t,f)\,df=\int _{t-B}^{t+B}x(\tau )\int _{-\infty }^{\infty }e^{-j2\pi f\tau }\,df\,d\tau =\int _{t-B}^{t+B}x(\tau )\delta (\tau )\,d\tau ={\begin{cases}\ x(0);&|t|<B\\\ 0;&{\text{otherwise}}\end{cases}}}$

(b)

${\displaystyle \int _{-\infty }^{\infty }X(t,f)e^{-j2\pi fv}\,df={\begin{cases}\ x(v);&v-B<t<v+B\\\ 0;&{\text{otherwise}}\end{cases}}}$

• Shifting property(shift along x-axis)

${\displaystyle \int _{t-B}^{t+B}x(\tau +\tau _{0})e^{-j2\pi f\tau }\,d\tau =X(t+\tau _{0},f)e^{j2\pi f\tau _{0}}}$

• Modulation property (shift along y-axis)

${\displaystyle \int _{t-B}^{t+B}[x(\tau )e^{j2\pi f_{0}\tau }]d\tau =X(t,f-f_{0})}$

• special input

1. When ${\displaystyle x(t)=\delta (t),X(t,f)={\begin{cases}\ 1;&|t|<B\\\ 0;&{\text{otherwise}}\end{cases}}}$
2. When ${\displaystyle x(t)=1,X(t,f)=2B\operatorname {sinc} (2Bf)e^{j2\pi ft}}$

• Linearity property

If ${\displaystyle h(t)=\alpha x(t)+\beta y(t)\,}$,${\displaystyle H(t,f),X(t,f),}$and ${\displaystyle Y(t,f)\,}$are their rec-STFTs, then

${\displaystyle H(t,f)=\alpha X(t,f)+\beta Y(t,f).}$

• Power integration property

${\displaystyle \int _{-\infty }^{\infty }|X(t,f)|^{2}\,df=\int _{t-B}^{t+B}|x(\tau )|^{2}\,d\tau }$

${\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|X(t,f)|^{2}\,df\,dt=2B\int _{-\infty }^{\infty }|x(\tau )|^{2}\,d\tau }$

• Energy sum property(Parseval's theorem)

${\displaystyle \int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df=\int _{t-B}^{t+B}x(\tau )y^{*}(\tau )\,d\tau }$

${\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df\,dt=2B\int _{-\infty }^{\infty }x(\tau )y^{*}(\tau )\,d\tau }$

Rectangular mask B's effect

comparison of different B

From the image, when B is smaller, the time resolution is better. Otherwise, when B is larger, the frequency resolution is better.

We can choose specified B to decide time resolution and frequency resolution.

Advantage and disadvantage

• Compare with the Fourier transform

Advantage The instantaneous frequency can be observed.

Disadvantage Higher complexity of computation.

• Compared with other types of time-frequency analysis:

The rec-STFT has an advantage of the least computation time for digital implementation, but its performance is worse than other types of time-frequency analysis.

See also

• Uncertainty principle

References

1. Jian-Jiun Ding (2014) Time-frequency analysis and wavelet transform