Random coordinate descent
Randomized (Block) Coordinate Descent Method is an optimization algorithm popularized by Nesterov (2010) and Richtárik and Takáč (2011). The first analysis of this method, when applied to the problem of minimizing a smooth convex function, was performed by Nesterov (2010).[1] In Nesterov's analysis the method needs to be applied to a quadratic perturbation of the original function with an unknown scaling factor. Richtárik and Takáč (2011) give iteration complexity bounds which do not require this, i.e., the method is applied to the objective function directly. Furthermore, they generalize the setting to the problem of minimizing a composite function, i.e., sum of a smooth convex and a (possibly nonsmooth) convex block-separable function:
where is decomposed into blocks of variables/coordinates: and are (simple) convex functions.
Example (block decomposition): If and , one may choose and .
Example (block-separable regularizers):
- , where and is the standard Euclidean norm.
Algorithm
Consider the optimization problem
where is a convex and smooth function.
Smoothness: By smoothness we mean the following: we assume the gradient of is coordinate-wise Lipschitz continuous with constants . That is, we assume that
for all and , where denotes the partial derivative with respect to variable .
Nesterov, and Richtarik and Takac showed that the following algorithm converges to the optimal point:
Algorithm Random Coordinate Descent Method
Input: //starting point
Output:
set x := x_0
for k := 1, ... do
choose coordinate , uniformly at random
update
end for
- "←" denotes assignment. For instance, "largest ← item" means that the value of largest changes to the value of item.
- "return" terminates the algorithm and outputs the following value.
Convergence rate
Since the iterates of this algorithm are random vectors, a complexity result would give a bound on the number of iterations needed for the method to output an approximate solution with high probability. It was shown in [2] that if , where , is an optimal solution (), is a confidence level and is target accuracy, then .
Example on particular function
The following Figure shows how develops during iterations, in principle. The problem is
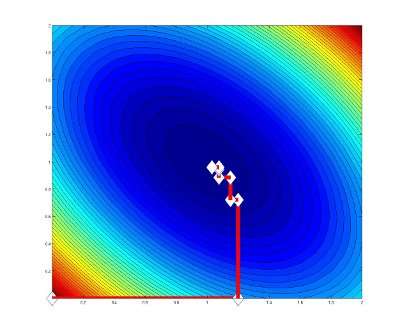
Extension to block coordinate setting
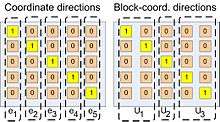
One can naturally extend this algorithm not only just to coordinates, but to blocks of coordinates. Assume that we have space . This space has 5 coordinate directions, concretely in which Random Coordinate Descent Method can move. However, one can group some coordinate directions into blocks and we can have instead of those 5 coordinate directions 3 block coordinate directions (see image).
References
- Nesterov, Yurii (2010), "Efficiency of coordinate descent methods on huge-scale optimization problems", SIAM Journal on Optimization, 22 (2): 341–362, CiteSeerX 10.1.1.332.3336, doi:10.1137/100802001
- Richtárik, Peter; Takáč, Martin (2011), "Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function", Mathematical Programming, Series A, 144 (1–2): 1–38, arXiv:1107.2848, doi:10.1007/s10107-012-0614-z