Radiodrome

In geometry, a radiodrome is the pursuit curve followed by a point that is pursuing another linearly-moving point. The term is derived from the Greek words ῥᾴδιος, rhā́idios, 'easier' and δρόμος, drómos, 'running'. The classic (and best-known) form of a radiodrome is known as the "dog curve"; this is the path a dog follows when it swims across a stream with a current after something it has spotted on the other side. Because the dog drifts with the current, it will have to change its heading; it will also have to swim further than if it had taken the optimal heading. This case was described by Pierre Bouguer in 1732.

A radiodrome may alternatively be described as the path a dog follows when chasing a hare, assuming that the hare runs in a straight line at a constant velocity.

The path of a dog chasing a hare running along a vertical straight line at a constant speed. The dog runs towards the momentary position of the hare, and will be changing his heading continuously.

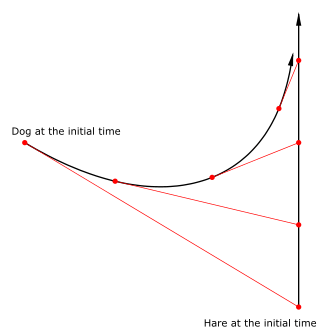
Mathematical analysis

Introduce a coordinate system with origin at the position of the dog at time zero and with y-axis in the direction the hare is running with the constant speed ${\displaystyle V_{t}}$. The position of the hare at time zero is (A_x, A_y) with A_x > 0 and at time t it is

${\displaystyle (T_{x}\ ,\ T_{y})\ =\ (A_{x}\ ,\ A_{y}+V_{t}t)}$

(1)

The dog runs with the constant speed ${\displaystyle V_{d}}$ towards the instantaneous position of the hare.

The differential equation corresponding to the movement of the dog, (x(t), y(t)), is consequently

${\displaystyle {\dot {x}}=V_{d}\ {\frac {T_{x}-x}{\sqrt {(T_{x}-x)^{2}+(T_{y}-y)^{2}}}}}$

(2)

${\displaystyle {\dot {y}}=V_{d}\ {\frac {T_{y}-y}{\sqrt {(T_{x}-x)^{2}+(T_{y}-y)^{2}}}}}$

(3)

It is possible to obtain a closed-form analytic expression y=f(x) for the motion of the dog, From (2) and (3) it follows that

${\displaystyle y'(x)={\frac {T_{y}-y}{T_{x}-x}}}$

(4)

Multiplying both sides with ${\displaystyle T_{x}-x}$ and taking the derivative with respect to x using that

${\displaystyle {\frac {dT_{y}}{dx}}\ =\ {\frac {dT_{y}}{dt}}\ {\frac {dt}{dx}}\ =\ {\frac {V_{t}}{V_{d}}}\ {\sqrt {{y'}^{2}+1}}}$

(5)

one gets

${\displaystyle y''={\frac {V_{t}\ {\sqrt {1+{y'}^{2}}}}{V_{d}(A_{x}-x)}}}$

(6)

or

${\displaystyle {\frac {y''}{\sqrt {1+{y'}^{2}}}}={\frac {V_{t}}{V_{d}(A_{x}-x)}}}$

(7)

From this relation it follows that

${\displaystyle \sinh ^{-1}(y')=B-{\frac {V_{t}}{V_{d}}}\ \ln(A_{x}-x)}$

(8)

where B is the constant of integration determined by the initial value of y' at time zero, y' (0)= sinh(B − (V_t /V_d) lnA_x), i.e.,

${\displaystyle B={\frac {V_{t}}{V_{d}}}\ \ln(A_{x})+\ln \left(y'(0)+{\sqrt {{y'(0)}^{2}+1}}\right)}$

(9)

From (8) and (9) it follows after some computations that

${\displaystyle y'={\frac {1}{2}}\left[\left(y'(0)+{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{-{\frac {V_{t}}{V_{d}}}}+\left(y'(0)-{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{\frac {V_{t}}{V_{d}}}\right]}$

(10)

Furthermore, since y(0)=0, it follows from (1) and (4) that

${\displaystyle y'(0)={\frac {A_{y}}{A_{x}}}}$

(11)

If, now, V_t ≠ V_d, relation (10) integrates to

${\displaystyle y=C-{\frac {A_{x}}{2}}\left[{\frac {\left(y'(0)+{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{1-{\frac {V_{t}}{V_{d}}}}}{1-{\frac {V_{t}}{V_{d}}}}}+{\frac {\left(y'(0)-{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{1+{\frac {V_{t}}{V_{d}}}}}{1+{\frac {V_{t}}{V_{d}}}}}\right]}$

(12)

where C is the constant of integration. Since again y(0)=0, it's

${\displaystyle C={\frac {A_{x}}{2}}\left[{\frac {y'(0)+{\sqrt {{y'(0)}^{2}+1}}}{1-{\frac {V_{t}}{V_{d}}}}}+{\frac {y'(0)-{\sqrt {{y'(0)}^{2}+1}}}{1+{\frac {V_{t}}{V_{d}}}}}\right]}$

(13)

The equations (11), (12) and (13) then together imply

${\displaystyle y={\frac {1}{2}}\left\{{\frac {A_{y}+{\sqrt {A_{x}^{2}+A_{y}^{2}}}}{1-{\frac {V_{t}}{V_{d}}}}}\left[1-\left(1-{\frac {x}{A_{x}}}\right)^{1-{\frac {V_{t}}{V_{d}}}}\right]+{\frac {A_{y}-{\sqrt {A_{x}^{2}+A_{y}^{2}}}}{1+{\frac {V_{t}}{V_{d}}}}}\left[1-\left(1-{\frac {x}{A_{x}}}\right)^{1+{\frac {V_{t}}{V_{d}}}}\right]\right\}}$

(14)

If V_t = V_d, relation (10) gives instead

${\displaystyle y=C-{\frac {A_{x}}{2}}\left[\left(y'(0)+{\sqrt {{y'(0)}^{2}+1}}\right)\ln \left(1-{\frac {x}{A_{x}}}\right)+{\frac {1}{2}}\left(y'(0)-{\sqrt {{y'(0)}^{2}+1}}\right)\left(1-{\frac {x}{A_{x}}}\right)^{2}\right]}$

(15)

Using y(0)=0 once again, it follows

${\displaystyle C={\frac {A_{x}}{4}}\left(y'(0)-{\sqrt {{y'(0)}^{2}+1}}\right)}$

(16)

The equations (11), (15) and (16) then together imply

${\displaystyle y={\frac {1}{4}}\left(A_{y}-{\sqrt {A_{x}^{2}+A_{y}^{2}}}\right)\left[1-\left(1-{\frac {x}{A_{x}}}\right)^{2}\right]-{\frac {1}{2}}\left(A_{y}+{\sqrt {A_{x}^{2}+A_{y}^{2}}}\right)\ln \left(1-{\frac {x}{A_{x}}}\right)}$

(17)

If V_t < V_d, it follows from (14) that

${\displaystyle \lim _{x\to A_{x}}y(x)={\frac {1}{2}}\left({\frac {A_{y}+{\sqrt {A_{x}^{2}+A_{y}^{2}}}}{1-{\frac {V_{t}}{V_{d}}}}}+{\frac {A_{y}-{\sqrt {A_{x}^{2}+A_{y}^{2}}}}{1+{\frac {V_{t}}{V_{d}}}}}\right)}$

(18)

If V_t ≥ V_d, one has from (14) and (17) that ${\displaystyle \lim _{x\to A_{x}}y(x)=\infty }$, which means that the hare will never be caught, whenever the chase starts.

See also

• Mice problem

References

• Nahin, Paul J. (2012), Chases and Escapes: The Mathematics of Pursuit and Evasion, Princeton: Princeton University Press, ISBN 978-0-691-12514-5.
• Gomes Teixera, Francisco (1909), Imprensa da universidade (ed.), Traité des Courbes Spéciales Remarquables, 2, Coimbra, p. 255