Radio coloring

In graph theory, a branch of mathematics, a radio coloring of an undirected graph is a form of graph coloring in which one assigns positive integer labels to the graphs such that the labels of adjacent vertices differ by at least two, and the labels of vertices at distance two from each other differ by at least one. Radio coloring was first studied by Griggs & Yeh (1992), under a different name, L(2,1)-labeling.[1][2] It was called radio coloring by Frank Harary because it models the problem of channel assignment in radio broadcasting, while avoiding electromagnetic interference between radio stations that are near each other both in the graph and in their assigned channel frequencies.

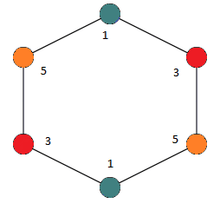
Optimal (span-5) radio coloring of a 6-cycle

The span of a radio coloring is its maximum label, and the radio coloring number of a graph is the smallest possible span of a radio coloring.[1] For instance, the graph consisting of two vertices with a single edge has radio coloring number 3: it has a radio coloring with one vertex labeled 1 and the other labeled 3, but it is not possible for a radio coloring of this graph to use only the labels 1 and 2.

Computational complexity

Finding a radio coloring with a given (or minimum) span is NP-complete, even when restricted to planar graphs, split graphs, or the complements of bipartite graphs.[1][3] However it is solvable in polynomial time for trees and cographs.[1][4] For arbitrary graphs, it can be solved in singly-exponential time, significantly faster than a brute-force search through all possible colorings.[5][6]

Other properties

Although the radio coloring number of an n-vertex graph can range from 1 to 2n − 1, almost all n-vertex graphs have radio coloring number exactly n. This is because these graphs almost always have diameter at least two (forcing all vertices to have distinct colors, and forcing the radio coloring number to be at least n) but they also almost always have a Hamiltonian path in the complement graph. Consecutive vertices in this path can be assigned consecutive colors, allowing a radio coloring to avoid skipping any numbers.[7]

gollark: What happened to that tamper-sensitive bomb idea?
gollark: Ice cream(m?) ≈ poop
gollark: Destroy it and everything it has ever contacted. But install potatOS first so I can "remote debug" it.
gollark: This must not be permitted to spread.
gollark: Have you tried nuking it from orbit?

References
  1. Broersma, Hajo (2005), "A general framework for coloring problems: old results, new results, and open problems" (PDF), Combinatorial geometry and graph theory, Lecture Notes in Comput. Sci., 3330, Springer, Berlin, pp. 65–79, doi:10.1007/978-3-540-30540-8_7, MR 2172960. See in particular Section 3, "Radio coloring".
  2. Griggs, Jerrold R.; Yeh, Roger K. (1992), "Labelling graphs with a condition at distance 2", SIAM Journal on Discrete Mathematics, 5 (4): 586–595, doi:10.1137/0405048, MR 1186826.
  3. Bodlaender, Hans L.; Kloks, Ton; Tan, Richard B.; van Leeuwen, Jan (2000), "λ-coloring of graphs", STACS 2000: 17th Annual Symposium on Theoretical Aspects of Computer Science, Lille, France, February 17–19, 2000, Proceedings, Lecture Notes in Computer Science, 1770, Springer, Berlin, pp. 395–406, doi:10.1007/3-540-46541-3_33, MR 1781749.
  4. Chang, Gerard J.; Kuo, David (1996), "The L(2,1)-labeling problem on graphs", SIAM Journal on Discrete Mathematics, 9 (2): 309–316, CiteSeerX 10.1.1.51.2004, doi:10.1137/S0895480193245339, MR 1386886.
  5. Havet, Frédéric; Klazar, Martin; Kratochvíl, Jan; Kratsch, Dieter; Liedloff, Mathieu (2011), "Exact algorithms for L(2,1)-labeling of graphs", Algorithmica, 59 (2): 169–194, doi:10.1007/s00453-009-9302-7, MR 2765572.
  6. Junosza-Szaniawski, Konstanty; Rzążewski, Paweł (2011), "On the complexity of exact algorithm for L(2,1)-labeling of graphs", Information Processing Letters, 111 (14): 697–701, doi:10.1016/j.ipl.2011.04.010, MR 2840535.
  7. Harary, Frank; Plantholt, Michael (1999), "Graphs whose radio coloring number equals the number of nodes", Graph colouring and applications (Montréal, QC, 1997), CRM Proc. Lecture Notes, 23, Providence, RI: American Mathematical Society, pp. 99–100, MR 1723637.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.