Pseudo great rhombicuboctahedron

In geometry, the pseudo great rhombicuboctahedron is one of the two pseudo uniform polyhedra, the other being the convex elongated square gyrobicupola or pseudo rhombicuboctahedron. It has the same vertex figure as the nonconvex great rhombicuboctahedron (a uniform polyhedron), but is not a uniform polyhedron (due to not being isogonal), and has a smaller symmetry group. It can be obtained from the great rhombicuboctahedron by taking a square face and the 8 faces with a common vertex to it (forming a crossed square cupola) and rotating them by an angle of ​π⁄4. It is related to the nonconvex great rhombicuboctahedron in the same way that the pseudo rhombicuboctahedron is related to the rhombicuboctahedron.

Pseudo great rhombicuboctahedron
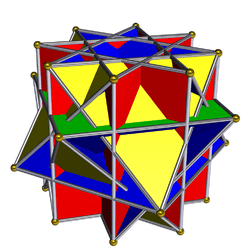TypePseudo uniform polyhedron,
Star polyhedron
ElementsF = 26, E = 48
V = 24 (χ = 2)
Faces by sides8{3}+(8+8+2){4}
Symmetry groupD4d
Propertiessingular vertex figure

4.4.4.3/2
Vertex figure
Pseudo great deltoidal icositetrahedron
(dual polyhedron)

The pseudo-great rhombicuboctahedron may also be termed an elongated crossed square gyrobicupola, in analogy to the name of the elongated square gyrobicupola.


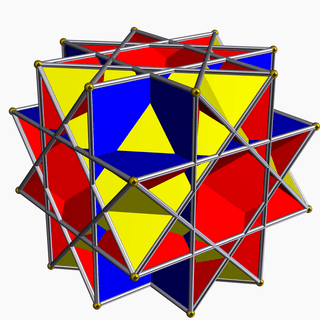Great rhombicuboctahedron
Pseudo great rhombicuboctahedron
gollark: That sure is a PCB of some sort.
gollark: But have you heard of H.266/VVC?
gollark: Yes.
gollark: Billions? Weak.
gollark: Everyone is possibly my alt. Claiming that they are and denying it on the alt helps quash those suspicions.

References
  • Grünbaum, Branko (2009). "An enduring error". Elemente der Mathematik. 64 (3): 89–101. doi:10.4171/EM/120. MR 2520469.CS1 maint: ref=harv (link). Reprinted in Pitici, Mircea, ed. (2011). The Best Writing on Mathematics 2010. Princeton University Press. pp. 18–31..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.