Probabilistic metric space

A probabilistic metric space is a generalization of metric spaces where the distance has no longer values in non-negative real numbers, but in distribution functions.

Let D+ be the set of all probability distribution functions F such that F(0) = 0 (F is a nondecreasing, left continuous mapping from ${\displaystyle \mathbb {R} }$ into [0, 1] such that max(F) = 1).

The ordered pair (S,F) is said to be a probabilistic metric space if S is a nonempty set and F: S×S → D+ (F(p, q) is denoted by F_p,q for every (p, q) ∈ S × S) satisfies the following conditions:

• F_u,v(x) = 1 for every x > 0 ⇔ u = v (u, v ∈ S).
• F_u,v = F_v,u for every u, v ∈ S.
• F_u,v(x) = 1 and F_v,w(y) = 1 ⇒ F_u,w(x + y) = 1 for u, v, w ∈ S and x, y ∈ R+.

Probability metric of random variables

A probability metric D between two random variables X and Y may be defined e.g. as:

${\displaystyle D(X,Y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|F(x,y)\,dxdy}$

where F(x, y) denotes the joint probability density function of random variables X and Y. Obviously if X and Y are independent from each other the equation above transforms into:

${\displaystyle D(X,Y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|f(x)g(y)\,dxdy}$

where f(x) and g(y) are probability density functions of X and Y respectively.

One may easily show that such probability metrics do not satisfy the first metric axiom or satisfies it if, and only if, both of arguments X and Y are certain events described by Dirac delta density probability distribution functions. In this case:

${\displaystyle D(X,Y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|\delta (x-\mu _{x})\delta (y-\mu _{y})\,dxdy=|\mu _{x}-\mu _{y}|}$

the probability metric simply transforms into the metric between expected values ${\displaystyle \mu _{x}}$, ${\displaystyle \mu _{y}}$ of the variables X and Y.

For all other random variables X, Y the probability metric does not satisfy the identity of indiscernibles condition required to be satisfied by the metric of the metric space, that is:

${\displaystyle D\left(X,X\right)>0}$

Probability metric between two random variables X and Y, both having normal distributions and the same standard deviation ${\displaystyle \sigma =0,\sigma =0.2,\sigma =0.4,\sigma =0.6,\sigma =0.8,\sigma =1}$ (beginning with the bottom curve). ${\displaystyle m_{xy}=|\mu _{x}-\mu _{y}|}$ denotes a distance between means of X and Y.

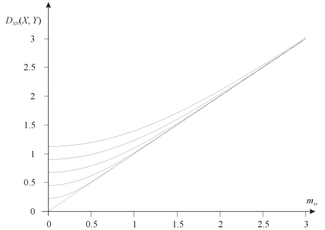
Example

For example if both probability distribution functions of random variables X and Y are normal distributions (N) having the same standard deviation ${\displaystyle \sigma }$, integrating ${\displaystyle D\left(X,Y\right)}$ yields to:

${\displaystyle D_{NN}(X,Y)=\mu _{xy}+{\frac {2\sigma }{\sqrt {\pi }}}\operatorname {exp} \left(-{\frac {\mu _{xy}^{2}}{4\sigma ^{2}}}\right)-\mu _{xy}\operatorname {erfc} \left({\frac {\mu _{xy}}{2\sigma }}\right)}$

where:

${\displaystyle \mu _{xy}=\left|\mu _{x}-\mu _{y}\right|}$,

and ${\displaystyle \operatorname {erfc} (x)}$ is the complementary error function.

In this case:

${\displaystyle \lim _{\mu _{xy}\to 0}D_{NN}(X,Y)=D_{NN}(X,X)={\frac {2\sigma }{\sqrt {\pi }}}}$

Probability metric of random vectors

The probability metric of random variables may be extended into metric D(X, Y) of random vectors X, Y by substituting ${\displaystyle |x-y|}$ with any metric operator d(x,y):

${\displaystyle D(\mathbf {X} ,\mathbf {Y} )=\int _{\Omega }\int _{\Omega }d(\mathbf {x} ,\mathbf {y} )F(\mathbf {x} ,\mathbf {y} )\,d\Omega _{x}d\Omega _{y}}$

where F(X, Y) is the joint probability density function of random vectors X and Y. For example substituting d(x,y) with Euclidean metric and providing the vectors X and Y are mutually independent would yield to:

${\displaystyle D(\mathbf {X} ,\mathbf {Y} )=\int _{\Omega }\int _{\Omega }{\sqrt {\sum _{i}|x_{i}-y_{i}|^{2}}}F(\mathbf {x} )G(\mathbf {y} )\,d\Omega _{x}d\Omega _{y}}$