Principal value

In mathematics, specifically complex analysis, the principal values of a multivalued function are the values along one chosen branch of that function, so that it is single-valued. The simplest case arises in taking the square root of a positive real number. For example, 4 has two square roots: 2 and –2; of these the positive root, 2, is considered the principal root and is denoted as ${\displaystyle {\sqrt {4}}.}$

For the use of the term principal value in describing improper integrals, see Cauchy principal value.

Motivation

Consider the complex logarithm function log z. It is defined as the complex number w such that

${\displaystyle e^{w}=z.}$

Now, for example, say we wish to find log i. This means we want to solve

${\displaystyle e^{w}=i}$

for w. Clearly iπ/2 is a solution. But is it the only solution?

Of course, there are other solutions, which is evidenced by considering the position of i in the complex plane and in particular its argument arg i. We can rotate counterclockwise π/2 radians from 1 to reach i initially, but if we rotate further another 2π we reach i again. So, we can conclude that i(π/2 + 2π) is also a solution for log i. It becomes clear that we can add any multiple of 2πi to our initial solution to obtain all values for log i.

But this has a consequence that may be surprising in comparison of real valued functions: log i does not have one definite value! For log z, we have

${\displaystyle \log {z}=\ln {|z|}+i\left(\mathrm {arg} \ z\right)=\ln {|z|}+i\left(\mathrm {Arg} \ z+2\pi k\right)}$

for an integer k, where Arg z is the (principal) argument of z defined to lie in the interval ${\displaystyle (-\pi ,\ \pi ]}$. As the principal argument is unique for a given complex number z, ${\displaystyle -\pi }$ is not included in the interval. Each value of k determines what is known as a branch (or sheet), a single-valued component of the multiple-valued log function.

The branch corresponding to k = 0 is known as the principal branch, and along this branch, the values the function takes are known as the principal values.

General case

In general, if f(z) is multiple-valued, the principal branch of f is denoted

${\displaystyle \mathrm {pv} \,f(z)}$

such that for z in the domain of f, pv f(z) is single-valued.

Principal values of standard functions

Complex valued elementary functions can be multiple-valued over some domains. The principal value of some of these functions can be obtained by decomposing the function into simpler ones whereby the principal value of the simple functions are straightforward to obtain.

Logarithm function

We have examined the logarithm function above, i.e.,

${\displaystyle \log {z}=\ln {|z|}+i\left(\mathrm {arg} \ z\right).}$

Now, arg z is intrinsically multivalued. One often defines the argument of some complex number to be between ${\displaystyle -\pi }$ (exclusive) and ${\displaystyle \pi }$ (inclusive), so we take this to be the principal value of the argument, and we write the argument function on this branch Arg z (with the leading capital A). Using Arg z instead of arg z, we obtain the principal value of the logarithm, and we write

${\displaystyle \mathrm {pv} \log {z}=\mathrm {Log} \,z=\ln {|z|}+i\left(\mathrm {Arg} \,z\right).}$

Square root

For a complex number ${\displaystyle z=re^{\phi i}\,}$ the principal value of the square root is:

${\displaystyle \mathrm {pv} {\sqrt {z}}={\sqrt {r}}\,e^{i\phi /2}}$

with argument ${\displaystyle -\pi <\phi \leq \pi .}$

Complex argument

comparison of atan and atan2 functions

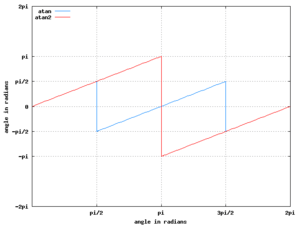
The principal value of complex number argument measured in radians can be defined as:

• values in the range ${\displaystyle [0,2\pi )}$
• values in the range ${\displaystyle (-\pi ,\pi ]}$

To compute these values one can use functions :

• atan2 with principal value in the range ${\displaystyle (-\pi ,\pi ]}$
• atan with principal value in the range ${\displaystyle ({\tfrac {-\pi }{2}},{\tfrac {\pi }{2}}]}$

See also

• Principal branch
• Branch point