Porphyrian tree

The Tree of Porphyry is a classic device for illustrating what is also called a "scale of being". It was suggested—if not first, then most famously in the European philosophical tradition—by the 3rd century CE Greek neoplatonist philosopher and logician Porphyry.[1] It is also known as scala praedicamentalis.

Three Porphyrian trees by Purchotius (1730), Boethius (6th century), and Ramon Llull (ca. 1305).

Porphyry suggests the Porphyrian tree in his introduction (in Greek, "Isagoge") to Aristotle's Categories. Porphyry presented Aristotle's classification of categories in a way that was later adopted into tree-like diagrams of two-way divisions, which indicate that a species is defined by a genus and a differentia and that this logical process continues until the lowest species is reached, which can no longer be so defined. No illustrations or diagrams occur in editions of Porphyry's original work. But, diagrams were eventually made, and became associated with the scheme that Porphyry describes, following Aristotle.

Porphyry's Isagoge was originally written in Greek, but was translated into Latin in the early 6th century CE by Boethius. Boethius's translation became the standard philosophical logic textbook in the Middle Ages.[2] Until the late 19th century, theories of categories based on Porphyry's work were still being taught to students of logic.

The following very helpful passage by philosopher James Franklin gives some hint as to the history of the Porphyrian tree:

In medieval education, the standard introduction to Aristotle's works was via Porphyry's Isagoge, and division entered the educated consciousness in the form of 'Porphyry's Tree'. It is not clear that Porphyry himself, in the relevant passage,[3] went any further than Aristotle in recommending division. But his brief comment was developed into the Tree by medieval logicians. It appears in William of Sherwood's Introduction to Logic and is given the name arbor Porphyrii in the most popular medieval logic, Peter of Spain's Summulae Logicales.[4] Linnaeus's system of static and discrete species was simply the result of filling in the abstract Tree with the names of actual species.[5]

Thus, the notion of the Porphyrian tree as an actual diagram comes later than Porphyry himself. Still, scholars do speak of Porphyry's tree as in the Isagoge and they mean by this only that the idea of dividing genera into species via differentiae is found in the Isagoge. But, of course, Porphyry was only following what was already in Aristotle, and Aristotle was following what was already in his teacher, Plato.[6]

Example

The following Porphyrian tree consists of three columns of words; the middlemost (in boldface) contains the series of genera and species, and we can take as analogous to the trunk of a tree. The extremes (the terms that jut out to the left and right), containing the differentiae, we can take as analogous to the branches of a tree:

This image is an illustration of the notion of a Porphyrian Tree as it comes down to us today through the European philosophical and logical tradition.

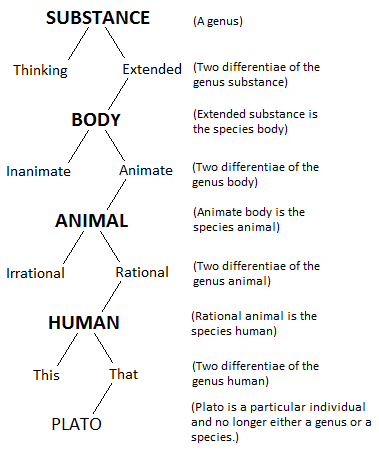
The diagram shows the highest genus to be substance. (Whether substance is a highest genus, really, is not in question here: right now we are only going to discuss what the diagram shows, not whether what it shows is true or false.) The technical term for a highest substance is summum genus. So, substance is the summum genus as far as this diagram goes. The diagram shows that the genus substance to have two differentia, namely, "thinking" and "extended". This indicates that there are two species of the genus substance, thinking substance and extended substance. The diagram does not give a term for the species of thinking substance (this would be "mind"), but it does give the term for the species of extended substance, namely, body. That is, body is a species of the genus substance; body is that species of the genus substance that is extended.

Now that we have seen body as a species of substance, we treat body as a genus itself. As a genus, it has two differentia of its own, inanimate and animate. So, there are two species of body, inanimate body and animate body. The diagram does not tell us what the term for inanimate body is, but it indicates a term for animate body, namely, animal. Animal is an animate species of the genus body.

And, again, now that we have looked at animal as a species of the genus body, we look at animal now as a genus and consider its differentia, which are shown on the diagram to be irrational and rational. Thus, according to the diagram there are two species of the genus animal, irrational animal and rational animal. We are not told by the diagram what a term for irrational animal is, but the diagram indicates that a rational animal is a human. Thus, human is a rational species of the genus animal.

Beneath human, however, there are no further species. "This" and "that" if they are considered differentiae, are of a special kind that map the species human not onto a new species but onto particular humans.,[7] The particular human Plato is named in the diagram. Plato is not a species (that is why his name is not in bold, unlike the species above). So, human is the lowest species in this diagram. The technical name for the lowest species in such a scheme is the infima species. So, for this diagram, human is the infima species.

See also

• Hierarchy
• Ontology
• Sefer ha-Ikkarim

Notes

1. James Franklin, "Aristotle on Species Variation", Philosophy, 61:236 (April 1986), pp. 245-252.
2. Stanford Encyclopedia of Philosophy - Medieval Theories of the Categories
3. Franklin's note: "Porphyry, Isagoge, trans. E. W. Warren (Toronto: Pontifical Institute of Medieval Studies, 1975), 34."
4. Franklin's note: "N. Kretzmann, William of Sherwood's Introduction to Logic (Minneapolis: University of Minnesota Press, 1966), 54; Peter of Spain, Summulae Logicales, I. M. Bocheński (ed.) (Turin: Marietti, 1947), 17-18."
5. James Franklin, "Aristotle on Species Variation", Philosophy, 61:236 (April 1986), pp. 245-252. The passage quoted here is from pp. 251-252.
6. A number of Plato's dialogs contain the idea of division in them: see Sophist, Philebus, Statesman, Republic (book VII), and Parmenides for starters.
7. For a discussion of "this" and "that" as universals/differentia, see G. W. F. Hegel, Phenomenology of Spirit, "A. Consciousness", "I. Sense-Certainty: or the 'this' and 'meaning' [Meinen]", translated by A. V. Miller, Oxford University Press, pp. 58-66.

References

 This article incorporates text from a publication now in the public domain: Chambers, Ephraim, ed. (1728). "Arbor Porphyriana". Cyclopædia, or an Universal Dictionary of Arts and Sciences (first ed.). James and John Knapton, et al. p. 128.

Further reading

Sources

• Porphyry, Isagoge (Porphyry's Introduction to Aristotle's 'Categories'.)
• Porphyry's Introduction, translation and commentary by Jonathan Barnes, Oxford, Oxford University Press, 2003.

Studies

• Asztalos, Monika. (1993). "Boethius as a Transmitter of Greek Logic to the Latin West: The Categories". Harvard Studies in Classical Philology, 95 (1993), pp. 367–407.
• Blum, Paul Richard. (1999). Dio e gli individui: L' Arbor Porphyriana nei secoli XVII e XVIII. Rivista di filosofia neo-scolastica 91: 18-49.
• Franklin, James. (1986). "Aristotle on Species Variation". Philosophy, 61:236 (April 1986), pp. 245–252.
• Kretzmann, Norman. (1966). William of Sherwood's Introduction to Logic (Minneapolis: University of Minnesota Press, 1966).
• Martin, John N. (2001). "Proclus and the Neoplatonic Syllogistic". Journal of Philosophical Logic, 30:3 (June 2001), pp. 187–240.
• Peter of Spain. (1947). Summulae Logicales, I. M. Bocheński (ed.) (Turin: Marietti, 1947).

External links

• Media related to Porphyrian tree at Wikimedia Commons