Pole figure

A pole figure is a graphical representation of the orientation of objects in space. For example, pole figures in the form of stereographic projections are used to represent the orientation distribution of crystallographic lattice planes in crystallography and texture analysis in materials science.

Definition
Poles of the faces of a cube

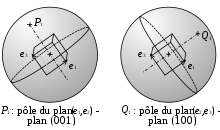
Consider an object with a basis attached to it. The orientation of the object in space can be determined by three rotations to transform the reference basis of space to the basis attached to the object; these are the Euler angles.

If we consider a plane of the object, the orientation of the plane can be given by its normal line. If we draw a sphere with the center on the plane, then

  • the intersection of the sphere and the plane is a circle, called the "trace" ;
  • the intersection of the normal line and the sphere is the pole.

A single pole is not enough to fully determine the orientation of an object: the pole stays the same if we apply a rotation around the normal line. The orientation of the object is fully determined by the use of poles of two planes that are not parallel.

Stereographic projection
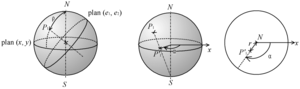
Stereographic projection of a pole

The upper sphere is projected on a plane using the stereographic projection.

Consider the (x,y) plane of the reference basis; its trace on the sphere is the equator of the sphere. We draw a line joining the South pole with the pole of interest P.

It is possible to choose any projection plane parallel to the equator (except the South pole): the figures will be proportional (property of similar triangles). It is usual to place the projection plane at the North pole.

Definition
The pole figure is the stereographic projection of the poles used to represent the orientation of an object in space.

Geometry in the pole figure
Wulff net, step of 10°
Wulff net, pole and trace of a plane
Pole figure of a diamond lattice in 111 direction.

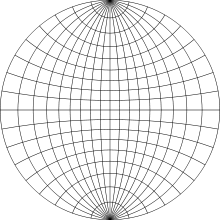
A Wulff net is used to read a pole figure.

The stereographic projection of a trace is an arc. The Wulff net is arcs corresponding to planes which share a common axis in the (x,y) plane.

If the pole and the trace of a plane are represented on the same diagram, then

  • we turn the Wulff net so the trace corresponds to an arc of the net;
  • the pole is situated on an arc, and the angular distance between this arc and the trace is 90°.

Consider an axis Δ, and planes belonging to the zone of this axis, i.e. Δ is in all these planes, the intersection of all the planes is Δ. If we call P the plane that is perpendicular to Δ, then the normals to the planes all belong to P. Thus, the poles of the planes belonging to the same zone are on the trace of the plane P perpendicular to the axis.

Application

Planes of a crystal

The structure of a crystal is often represented by the pole figure of its crystallographic plane.

A plane is chosen as the equator, usually the (001) or (011) plane; its pole is the center of the figure. Then, the poles of the other planes are placed on the figure, with the Miller indices for each pole. The poles that belong to a zone are sometimes linked with the related trace.

Texture
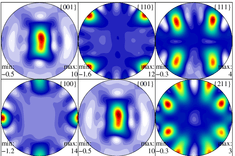
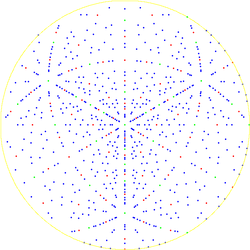
Pole figures displaying crystallographic texture of gamma-TiAl in an alpha2-gamma alloy, as measured by high energy X-rays.[1]

"Texture" in the context of Materials Science means "crystallographic preferred orientation". If a polycrystalline material (i.e. a material composed of many different crystals or grains, like most metals, ceramics or minerals) has "texture" then that means that the crystal axes are not randomly (or, more correctly, uniformly) distributed.

To draw a pole figure, one chooses a particular crystal direction (e.g. the normal to the (100) plane) and then plots that direction, called a pole, for each and every crystal relative to a set of directions in the material. In a rolled metal, for example, the directions in the material are the rolling direction, transverse direction and rolling plane normal.

If a large number of crystals are involved, then it is typical to make a contour plot, rather than plotting individual poles.

The full determination of the texture requires the plot of two pole figures corresponding to planes that are not parallel and that do not have the same diffraction angle (thus different interplanar distances).

Diffraction figure
Pole figure and diffraction figure

Consider the diffraction figure obtained with a single crystal, on a plane that is perpendicular to the beam, e.g. X-ray diffraction with the Laue method, or electron diffraction in a transmission electron microscope. The diffraction figure shows spots.

The position of the spots is determined by the Bragg's law. It gives the orientation of the plane.

If the parameters of the optics are known (especially the distance between the crystal and the photographic film), it is possible to build the stereographic diagram from the diffraction diagram, i.e. to transform the diffraction figure into a pole figure.

gollark: It's just so ææææææ.
gollark: If it wasn't for people needing to use different languages I would NOT support Unicode.
gollark: I have to admit I kind of agree?
gollark: > packed UTF-16 datawhich is bad but differently.
gollark: > (One reason for this policy of replacement is that internally, a Text value is represented as packed UTF-16 data. Values in the range U+D800 through U+DFFF are used by UTF-16 to denote surrogate code points, and so cannot be represented. The functions replace invalid scalar values, instead of dropping them, as a security measure. For details, see Unicode Technical Report 36, §3.5.)

References
  1. Liss KD, Bartels A, Schreyer A, Clemens H (2003). "High energy X-rays: A tool for advanced bulk investigations in materials science and physics". Textures Microstruct. 35 (3/4): 219–52. doi:10.1080/07303300310001634952.
  • Kocks, U. F., C. Tomé, and H.-R. Wenk, Eds. (1998). Texture and Anisotropy, Cambridge University Press, Cambridge, UK, ISBN 0-521-79420-X.
  • Val Randle and Olaf Engler (2000), Macrotexture, Microtexture & Orientation Mapping, Gordon & Breach, Amsterdam, Holland, ISBN 90-5699-224-4.
  • Adam Morawiec, Orientations and Rotations (2003), Springer, ISBN 3-540-40734-0.
  • Piotr Ozga, Pole Figures: Registration and Plot Conventions, http://www.labosoft.com.pl/pf_convention.pdf
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.