Poincaré–Miranda theorem

In mathematics, the Poincaré–Miranda theorem is a generalization of the intermediate value theorem, from a single function in a single dimension, to $n$ functions in $n$ dimensions. It says as follows:

Consider

n

continuous functions of

n

variables,

f_{1},\ldots ,f_{n}

. Assume that for each variable

x_{i}

, the function

f_{i}

is constantly negative when

x_{i}=-1

and constantly positive when

x_{i}=1

. Then there is a point in the

n

-dimensional cube

[-1,1]^{n}

in which all functions are simultaneously equal to

0

.

The theorem is named after Henri Poincaré, who conjectured it in 1883, and Carlo Miranda, who in 1940 showed that it is equivalent to the Brouwer fixed-point theorem.[1]

Intuitive description

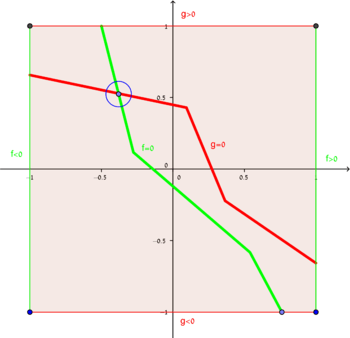
A graphical representation of Poincaré–Miranda theorem for

n = 2

The picture on the right shows an illustration of the Poincaré–Miranda theorem for $n = 2$ functions. Consider a couple of functions $(f, g)$ whose domain of definition is the $[-1,+1] 2$ square. The function $f$ is negative on the left boundary and positive on the right boundary (green sides of the square), while the function $g$ is negative on the lower boundary and positive on the upper boundary (red sides of the square). When we go from left to right along any path, we must go through a point in which $f$ is $0$ . Therefore, there must be a "wall" separating the left from the right, along which $f$ is $0$ (green curve inside the square). Similarly, there must be a "wall" separating the top from the bottom, along which $g$ is $0$ (red curve inside the square). These walls must intersect in a point in which both functions are $0$ (blue point inside the square).

Generalizations

The simplest generalization, as a matter of fact a corollary, of this theorem is the following one. For every variable $x i$ , let $a i$ be any value in the range $[sup x i = 0 f i, inf x i = 1 f i]$ . Then there is a point in the unit cube in which for all $i$ :

f_{i}=a_{i}

.

The this statement can be reduced to the original one by a simple translation of axes,

x_{i}^{\prime }=x_{i}\qquad y_{i}^{\prime }=y_{i}-a_{i}\qquad \forall i\in \{1,\dots ,n\}

where

$x i$ are the coordinates in the domain of the function
$y i$ are the coordinates in the codomain of the function

Notes

(Kulpa 1997, p. 545).

gollark: If something is right beside the edge of the gamefield, you can't push it, right?

gollark: And you cannotpush thingsWHICH ARE ADJACENTto the WALL?

gollark: Wait, *is* water noun?

gollark: And water is noun, you see.

gollark: Well, you could make the water float.

References

Dugundji, James; Granas, Andrzej (2003), Fixed Point Theory, Springer Monographs in Mathematics, New York: Springer-Verlag, pp. xv+690, ISBN 0-387-00173-5, MR 1987179, Zbl 1025.47002
Kulpa, Wladyslaw (June 1997), "The Poincare-Miranda Theorem", The American Mathematical Monthly, 104 (6): 545–550, doi:10.2307/2975081, JSTOR 2975081, MR 1453657, Zbl 0891.47040.
Miranda, Carlo (1940), "Un'osservazione su un teorema di Brouwer", Bollettino dell'Unione Matematica Italiana, Serie 2 (in Italian), 3: 5–7, JFM 66.0217.01, MR 0004775, Zbl 0024.02203.

External links

Ahlbach, Connor Thomas (2013). "A Discrete Approach to the Poincare–Miranda Theorem (HMC Senior Theses)". Retrieved 18 May 2015.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] (Kulpa 1997, p. 545).