Pig (dice game)

Pig is a simple dice game first described in print by John Scarne in 1945.[1] As with many games of folk origin, Pig is played with many rule variations. Commercial variants of Pig include Pass the Pigs, Pig Dice,[2] and Skunk. Pig is commonly used by mathematics teachers to teach probability concepts.

Pig is one of a family of dice games described by Reiner Knizia as "jeopardy dice games". For jeopardy dice games, the dominant type of decision is whether or not to jeopardize previous gains by rolling for potential greater gains. Most jeopardy dice games can be further subdivided into two categories: jeopardy race games and jeopardy approach games. In jeopardy race games, the object is to be the first to meet or exceed a goal score (e.g. Pig, Pass the Pigs, Cosmic Wimpout, Can't Stop). In jeopardy approach games, the object is to most closely approach a goal score without exceeding it.[3]

Gameplay

Each turn, a player repeatedly rolls a die until either a 1 is rolled or the player decides to "hold":

  • If the player rolls a 1, they score nothing and it becomes the next player's turn.
  • If the player rolls any other number, it is added to their turn total and the player's turn continues.
  • If a player chooses to "hold", their turn total is added to their score, and it becomes the next player's turn.

The first player to score 100 or more points wins.

For example, the first player, Donald, begins a turn with a roll of 5. Donald could hold and score 5 points, but chooses to roll again. Donald rolls a 2, and could hold with a turn total of 7 points, but chooses to roll again. Donald rolls a 1, and must end his turn without scoring. The next player, Alexis, rolls the sequence 4-5-3-5-5, after which she chooses to hold, and adds her turn total of 22 points to her score.

Optimal play
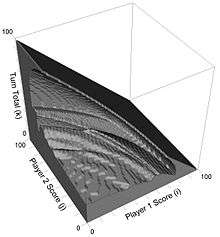
A visualisation of optimal play in the game of 2-player Pig

Optimal play for 2-player Pig was computed by Todd W. Neller[4] and visualized by Clifton G. M. Presser in 2001.[5] At any time, the relevant decision information includes the player's score, the opponent's score, and the turn total. Such information corresponds to a 3D point in the graph's space. If this point is inside the gray solid, the player should roll. Otherwise, the player should hold.

Many 2-dice variants have been analysed,[6] and human-playable Pig strategies have been compared to optimal play.[7]

Variations

Common rule variations include:[8]

  • Two dice: two dice are rolled instead of one (See "Two Dice Pig" below)
  • Any number of dice ("Hog" variation): the player rolls only once per turn with an arbitrary number of dice.
  • 6 is bad: a roll of 6 is treated as a roll of 1.

Two-Dice Pig

This variation is the same as Pig, except:

  • Two standard dice are rolled. If neither shows a 1, their sum is added to the turn total.
  • If a single 1 is rolled, the player scores nothing and the turn ends.
  • If two 1s are rolled, the player’s entire score is lost, and the turn ends.
  • If a double is rolled, the point total is added to the turn total as with any roll but the player is obligated to roll again (possible sub-variation of the two-dice game)

Big Pig

This variation is the same as Two-Dice Pig, except:

  • If two 1s are rolled, the player adds 25 to the turn total.
  • If other doubles are rolled, the player adds twice the value of the dice to the turn total.

Skunk

Skunk (or Think) is a variation of Two-Dice Pig that is played with large groups. Rather than rolling in turn, all players begin the round standing. At any point in the round, a player may hold by sitting down. The round continues until a 1 is rolled, or all players have sat down. Skunk is played in five rounds, and scoring is recorded in a 5-column table with columns labeled with the letters of the word "SKUNK". The first round score is entered in the "S"-column, the next in the first "K"-column, and so on. After five rounds, the highest-scoring player is the winner.[9]

Teaching

Pig often serves as a simple example for teaching probability concepts from the middle school level upwards. The game also provides exercises for teaching Computer Science in areas ranging from introductory courses to advanced machine learning material.[10]

gollark: If you just allocated the vote *randomly*, that would satisfy neither group, and is bad.
gollark: Actually, it's the opposite.
gollark: Just because both sides don't like something doesn't make it good.
gollark: You just get politicians focusing on a small subset of states which have lots of EC votes and are not always going to be a majority for one party.
gollark: So it does not, in fact, provide equally powerful voices per state.

References
  1. Scarne, John (1945). Scarne on Dice. Harrisburg, Pennsylvania: Military Service Publishing Co.
  2. Pig at BoardGameGeek
  3. Reiner Knizia, Dice Games Properly Explained. Elliot Right-Way Books, 1999
  4. Todd W. Neller and Clifton G.M. Presser. Optimal Play of the Dice Game Pig, The UMAP Journal 25(1) (2004), pp. 25–47.
  5. http://cs.gettysburg.edu/projects/pig/pigVis.html
  6. Todd W. Neller and Clifton G.M. Presser. Pigtail: A Pig Addendum, The UMAP Journal 26(4) (2005), pp. 443–458.
  7. Todd W. Neller and Clifton G.M. Presser. Practical Play of the Dice Game Pig, The UMAP Journal 31(1) (2010), pp. 5–19.
  8. http://cs.gettysburg.edu/projects/pig/piglinks.html
  9. http://illuminations.nctm.org/index_d.aspx?id=248
  10. Todd W. Neller, Clifton G.M. Presser, Ingrid Russell, Zdravko Markov. Pedagogical Possibilities for the Dice Game Pig. Journal of Computing Sciences in Colleges, vol. 21, no. 6, pp. 149–161, June 2006.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.