Persymmetric matrix
The first definition is the most common in the recent literature. The designation "Hankel matrix" is often used for matrices satisfying the property in the second definition.
In mathematics, persymmetric matrix may refer to:
- a square matrix which is symmetric with respect to the northeast-to-southwest diagonal; or
- a square matrix such that the values on each line perpendicular to the main diagonal are the same for a given line.
Definition 1
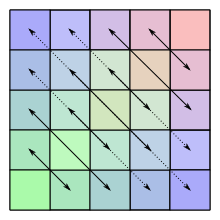
Let A = (aij) be an n × n matrix. The first definition of persymmetric requires that
- for all i, j.[1]
For example, 5-by-5 persymmetric matrices are of the form
This can be equivalently expressed as AJ = JAT where J is the exchange matrix.
A symmetric matrix is a matrix whose values are symmetric in the northwest-to-southeast diagonal. If a symmetric matrix is rotated by 90°, it becomes a persymmetric matrix. Symmetric persymmetric matrices are sometimes called bisymmetric matrices.
Definition 2
The second definition is due to Thomas Muir.[2] It says that the square matrix A = (aij) is persymmetric if aij depends only on i + j. Persymmetric matrices in this sense, or Hankel matrices as they are often called, are of the form
A persymmetric determinant is the determinant of a persymmetric matrix.[2]
A matrix for which the values on each line parallel to the main diagonal are constant, is called a Toeplitz matrix.
See also
References
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Baltimore: Johns Hopkins, ISBN 978-0-8018-5414-9. See page 193.
- Muir, Thomas (1960), Treatise on the Theory of Determinants, Dover Press, p. 419