Perpendicular bisector construction of a quadrilateral
In geometry, the perpendicular bisector construction of a quadrilateral is a construction which produces a new quadrilateral from a given quadrilateral using the perpendicular bisectors to the sides of the former quadrilateral. This construction arises naturally in an attempt to find a replacement for the circumcenter of a quadrilateral in the case that is non-cyclic.
Definition of the construction
Suppose that the vertices of the quadrilateral are given by . Let be the perpendicular bisectors of sides respectively. Then their intersections , with subscripts considered modulo 4, form the consequent quadrilateral . The construction is then iterated on to produce and so on.
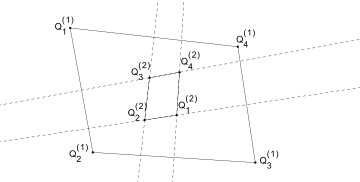
An equivalent construction can be obtained by letting the vertices of be the circumcenters of the 4 triangles formed by selecting combinations of 3 vertices of .
Properties
1. If is not cyclic, then is not degenerate.[1]
2. Quadrilateral is never cyclic.[1] Combining #1 and #2, is always nondegenrate.
3. Quadrilaterals and are homothetic, and in particular, similar.[2] Quadrilaterals and are also homothetic.
3. The perpendicular bisector construction can be reversed via isogonal conjugation.[3] That is, given , it is possible to construct .
4. Let be the angles of . For every , the ratio of areas of and is given by[3]
5. If is convex then the sequence of quadrilaterals converges to the isoptic point of , which is also the isoptic point for every . Similarly, if is concave, then the sequence obtained by reversing the construction converges to the Isoptic Point of the 's.[3]
References
- J. King, Quadrilaterals formed by perpendicular bisectors, in Geometry Turned On, (ed. J. King), MAA Notes 41, 1997, pp. 29–32.
- G. C. Shephard, The perpendicular bisector construction, Geom. Dedicata, 56 (1995) 75–84.
- O. Radko and E. Tsukerman, The Perpendicular Bisector Construction, the Isoptic Point and the Simson Line of a Quadrilateral, Forum Geometricorum 12: 161–189 (2012).
- J. Langr, Problem E1050, Amer. Math. Monthly, 60 (1953) 551.
- V. V. Prasolov, Plane Geometry Problems, vol. 1 (in Russian), 1991; Problem 6.31.
- V. V. Prasolov, Problems in Plane and Solid Geometry, vol. 1 (translated by D. Leites), available at http://students.imsa.edu/~tliu/math/planegeo.eps%5B%5D.
- D. Bennett, Dynamic geometry renews interest in an old problem, in Geometry Turned On, (ed. J. King), MAA Notes 41, 1997, pp. 25–28.
- J. King, Quadrilaterals formed by perpendicular bisectors, in Geometry Turned On, (ed. J. King), MAA Notes 41, 1997, pp. 29–32.
- G. C. Shephard, The perpendicular bisector construction, Geom. Dedicata, 56 (1995) 75–84.
- A. Bogomolny, Quadrilaterals formed by perpendicular bisectors, Interactive Mathematics Miscellany and Puzzles, http://www.cut-the-knot.org/Curriculum/Geometry/PerpBisectQuadri.shtml.
- B. Grünbaum, On quadrangles derived from quadrangles—Part 3, Geombinatorics 7(1998), 88–94.
- O. Radko and E. Tsukerman, The Perpendicular Bisector Construction, the Isoptic Point and the Simson Line of a Quadrilateral, Forum Geometricorum 12: 161–189 (2012).