Pedal triangle

In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle.

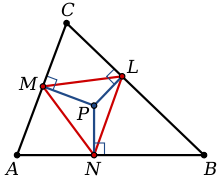
A triangle ABC in black, the perpendiculars from a point P in blue, and the obtained pedal triangle LMN in red.

More specifically, consider a triangle ABC, and a point P that is not one of the vertices A, B, C. Drop perpendiculars from P to the three sides of the triangle (these may need to be produced, i.e., extended). Label L, M, N the intersections of the lines from P with the sides BC, AC, AB. The pedal triangle is then LMN.

The location of the chosen point P relative to the chosen triangle ABC gives rise to some special cases:

The case when P is on the circumcircle, and the pedal triangle degenerates into a line (red).

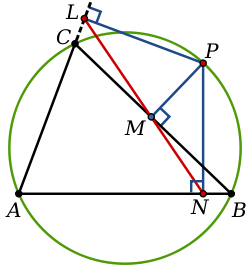
If P is on the circumcircle of the triangle, LMN collapses to a line. This is then called the pedal line, or sometimes the Simson line after Robert Simson.

The vertices of the pedal triangle of an interior point P, as shown in the top diagram, divide the sides of the original triangle in such a way as to satisfy Carnot's theorem:[1]

Trilinear coordinates

If P has trilinear coordinates p : q : r, then the vertices L,M,N of the pedal triangle of P are given by

  • L = 0 : q + p cos C : r + p cos B
  • M = p + q cos C : 0 : r + q cos A
  • N = p + r cos B : q + r cos A : 0

Antipedal triangle

One vertex, L', of the antipedal triangle of P is the point of intersection of the perpendicular to BP through B and the perpendicular to CP through C. Its other vertices, M ' and N ', are constructed analogously. Trilinear coordinates are given by

  • L' = − (q + p cos C)(r + p cos B) : (r + p cos B)(p + q cos C) : (q + p cos C)(p + r cos B)
  • M' = (r + q cos A)(q + p cos C) : − (r + q cos A)(p + q cos C) : (p + q cos C)(q + r cos A)
  • N' = (q + r cos A)(r + p cos B) : (p + r cos B)(r + q cos A) : − (p + r cos B)(q + r cos A)

For example, the excentral triangle is the antipedal triangle of the incenter.

Suppose that P does not lie on any of the extended sides BC, CA, AB, and let P−1 denote the isogonal conjugate of P. The pedal triangle of P is homothetic to the antipedal triangle of P−1. The homothetic center (which is a triangle center if and only if P is a triangle center) is the point given in trilinear coordinates by

ap(p + q cos C)(p + r cos B) : bq(q + r cos A)(q + p cos C) : cr(r + p cos B)(r + q cos A).

The product of the areas of the pedal triangle of P and the antipedal triangle of P−1 equals the square of the area of triangle ABC.

gollark: (like many CC programs)
gollark: Cool, although crazy.
gollark: Does it involve placing a binary file on the actual CC FS to hold all the file stuff or what?
gollark: Your CC OS supports ext2?
gollark: If they were to take it down, though, expect massive public backlash (unless it takes place ages from now), not that that will change much.

References
  1. Alfred S. Posamentier; Charles T. Salkind (1996). Challenging problems in geometry. New York: Dover. pp. 85-86. ISBN 9780486134864. OCLC 829151719.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.