Pearcey integral
In mathematics, the Pearcey[1] integral[2] is defined as[3]
The Pearcey integral is a class of canonical diffraction integrals, often used in wave propagation and optical diffraction problems[4]
In optics, the Pearcey integral can be used to model diffraction effects at a cusp caustic.

A photograph of a cusp caustic produced by illuminating a flat surface with a laser beam through a droplet of water.
Graphs
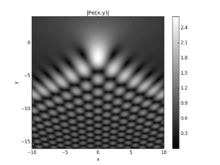
A plot of the absolute value of the Pearcey integral as a function of its two parameters.
gollark: *But* this is a bug in the JSON handling, which I should really fix *anyway*.
gollark: Ah, base64 should do it, yes.
gollark: Ah, *this* is the problem! The parser is primitive and does not support `\uxxxx`.
gollark: The problem is:* Lua bytestrings being encoded as JSON strings requires correct encoding* The JSON library didn't serialize that way* It appears to not *de*serialize that way? I don't know.
gollark: Er, hmm, that makes a bit of sense.
References
- https://csiropedia.csiro.au/Pearcey-Trevor/
- T. Pearcey, The structure of an electromagnetic field in the neighbourhood of a cusp of a caustic, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 37, 311-317, 1946
- Frank W. J. Olver, Daniel W. Lozier, Ronald F. Boisvert, Charles W. Clark, NIST Handbook of Mathematical Functions, p. 777, Cambridge, 2010
- R.B.Paris, Hadamard Expansions and Hyperasymptotic Evaluation, p. 207, Encyclopedia of Mathematics and its Applications, 141, Cambridge, 2011
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.