Spin isomers of hydrogen

Molecular hydrogen occurs in two isomeric forms, one with its two proton nuclear spins aligned parallel (orthohydrogen), the other with its two proton spins aligned antiparallel (parahydrogen).[1] These two forms are often referred to as spin isomers.[2]

Spin isomers of molecular hydrogen

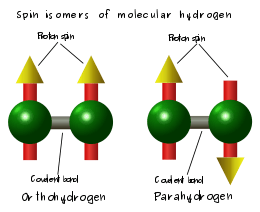
Parahydrogen is in a lower energy state than is orthohydrogen. At room temperature and thermal equilibrium, thermal excitation causes hydrogen to consist of approximately 75% orthohydrogen and 25% parahydrogen. When hydrogen is liquified at low temperature, there is a slow spontaneous transition to a predominantly para ratio, with the released energy having implications for storage. Essentially pure parahydrogen form can be obtained at very low temperatures, but it is not possible to obtain a sample containing more than 75% orthohydrogen by heating.

A mixture or 50:50 mixture of ortho- and parahydrogen can be made in the laboratory by passing it over an iron(III) oxide catalyst at liquid nitrogen temperature (77 K)[3] or by storing hydrogen at 77 K for 2–3 hours in the presence of activated charcoal.[4] In the absence of a catalyst, gas phase parahydrogen takes days to relax to normal hydrogen at room temperature while it takes hours to do so in organic solvents.[4]

Nuclear spin states of H₂

Each hydrogen molecule (H₂) consists of two hydrogen atoms linked by a covalent bond. If we neglect the small proportion of deuterium and tritium which may be present, each hydrogen atom consists of one proton and one electron. Each proton has an associated magnetic moment, which is associated with the proton's spin of ½. In the H₂ molecule, the spins of the two hydrogen nuclei (protons) couple to form a triplet state known as orthohydrogen, and a singlet state known as parahydrogen.

The triplet orthohydrogen state has total nuclear spin I = 1 so that the component along a defined axis can have the three values M_I = 1, 0, or −1. The corresponding nuclear spin wavefunctions are ${\displaystyle \left|\uparrow \uparrow \right\rangle }$, ${\displaystyle \textstyle {\frac {1}{\sqrt {2}}}(\left|\uparrow \downarrow \right\rangle +\left|\downarrow \uparrow \right\rangle )}$ and ${\displaystyle \left|\downarrow \downarrow \right\rangle }$. This uses standard bra–ket notation; the symbol ↑ represents the spin-up wavefunction and the symbol ↓ the spin-down wavefunction, so ↑↓ means that the first nucleus is up and the second down. Each orthohydrogen energy level then has a (nuclear) spin degeneracy of three, meaning that it corresponds to three states of the same energy (in the absence of a magnetic field).[1] The singlet parahydrogen state has nuclear spin quantum numbers I = 0 and M_I = 0, with wavefunction ${\displaystyle \textstyle {\frac {1}{\sqrt {2}}}(\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle )}$. Since there is only one possibility, each parahydrogen level has a spin degeneracy of one and is said to be non-degenerate.[1]

Allowed rotational energy levels

Since protons have spin ½, they are fermions and the permutational antisymmetry of the total H₂ wavefunction imposes restrictions on the possible rotational states the two forms of H₂.[1] Orthohydrogen, with symmetric nuclear spin functions, can only have rotational wavefunctions that are antisymmetric with respect to permutation of the two protons, corresponding to odd values of the rotational quantum number J; conversely, parahydrogen with an antisymmetric nuclear spin function, can only have rotational wavefunctions that are symmetric with respect to permutation of the two protons, corresponding to even J.[1]

The para form whose lowest level is J = 0 is more stable by 1.06 kJ/mol[5] than the ortho form whose lowest level is J = 1. The ratio between numbers of ortho and para molecules is about 3:1 at standard temperature where many rotational energy levels are populated, favoring the ortho form as a result of thermal energy. However at low temperatures only the J = 0 level is appreciably populated, so that the para form dominates at low temperatures (approx. 99.8% at 20 K).[6] The heat of vaporization is only 0.904 kJ/mol. As a result,[5] ortho liquid hydrogen equilibrating to the para form releases enough energy to cause significant loss by boiling.

Thermal properties

Applying the rigid rotor approximation, the energies and degeneracies of the rotational states are given by:[7]

${\displaystyle E_{J}={\frac {J(J+1)\hbar ^{2}}{2I}};\quad g_{J}=2J+1}$.

The rotational partition function is conventionally written as:

${\displaystyle Z_{\text{rot}}=\sum \limits _{J=0}^{\infty }{g_{J}e^{-E_{J}/k_{\text{B}}T\;}}}$.

However, as long as the two spin isomers are not in equilibrium, it is more useful to write separate partition functions for each:

${\displaystyle {\begin{aligned}Z_{\text{para}}&=\sum \limits _{{\text{even }}J}{(2J+1)e^{{-J(J+1)\hbar ^{2}}/{2Ik_{\text{B}}T}\;}}\\Z_{\text{ortho}}&=3\sum \limits _{{\text{odd }}J}{(2J+1)e^{{-J(J+1)\hbar ^{2}}/{2Ik_{\text{B}}T}\;}}\end{aligned}}}$

The factor of 3 in the partition function for orthohydrogen accounts for the spin degeneracy associated with the +1 spin state; when equilibrium between the spin isomers is possible, then a general partition function incorporating this degeneracy difference can be written as:

${\displaystyle Z_{\text{equil}}=\sum \limits _{J=0}^{\infty }{\left(2-(-1)^{J}\right)(2J+1)e^{{-J(J+1)\hbar ^{2}}/{2Ik_{\text{B}}T}\;}}}$

The molar rotational energies and heat capacities are derived for any of these cases from:

${\displaystyle {\begin{aligned}U_{\text{rot}}&=RT^{2}\left({\frac {\partial \ln Z_{\text{rot}}}{\partial T}}\right)\\C_{v,{\text{ rot}}}&={\frac {\partial U_{\text{rot}}}{\partial T}}\end{aligned}}}$

Plots shown here are molar rotational energies and heat capacities for ortho- and parahydrogen, and the "normal" ortho/para (3:1) and equilibrium mixtures:

Molar rotational energies

Molar heat capacities; only rotational and spin contribution is shown. Total value is 1.5R higher due to translational degrees of freedom (rotational degrees were included in the rigid rotor approximation itself).

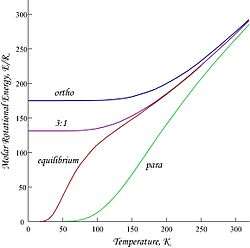
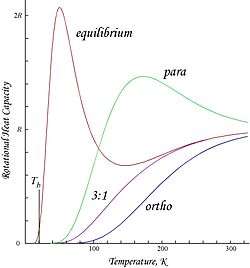
Because of the antisymmetry-imposed restriction on possible rotational states, orthohydrogen has residual rotational energy at low temperature wherein nearly all the molecules are in the J = 1 state (molecules in the symmetric spin-triplet state cannot fall into the lowest, symmetric rotational state) and possesses nuclear-spin entropy due to the triplet state's threefold degeneracy. The residual energy is significant because the rotational energy levels are relatively widely spaced in H₂; the gap between the first two levels when expressed in temperature units is twice the characteristic rotational temperature for H₂:

${\displaystyle {\frac {E_{J=1}-E_{J=0}}{k_{\text{B}}}}=2\theta _{\text{rot}}={\frac {\hbar ^{2}}{k_{\text{B}}I}}\approx 174.98{\text{ K}}}$.

This is the T = 0 intercept seen in the molar energy of orthohydrogen. Since "normal" room-temperature hydrogen is a 3:1 ortho:para mixture, its molar residual rotational energy at low temperature is (3/4) × 2Rθ_rot ≈ 1091 J/mol, which is somewhat larger than the enthalpy of vaporization of normal hydrogen, 904 J/mol at the boiling point, T_b ≈ 20.369 K.[8] Notably, the boiling points of parahydrogen and normal (3:1) hydrogen are nearly equal; for parahydrogen ∆H_vap ≈ 898 J/mol at T_b ≈ 20.277 K, and it follows that nearly all the residual rotational energy of orthohydrogen is retained in the liquid state.

However, orthohydrogen is thermodynamically unstable at low temperatures and spontaneously converts into parahydrogen.[9] This process lacks any natural de-excitation radiation mode, so it is slow in the absence of a catalyst which can facilitate interconversion of the singlet and triplet spin states.[10] At room temperature, hydrogen contains 75% orthohydrogen, a proportion which the liquefaction process preserves if carried out in the absence of a catalyst like ferric oxide, activated carbon, platinized asbestos, rare earth metals, uranium compounds, chromic oxide, or some nickel compounds to accelerate the conversion of the liquid hydrogen into parahydrogen. Alternatively, additional refrigeration equipment can be used to slowly absorb the heat that the orthohydrogen fraction will (more slowly) release as it spontaneously converts into parahydrogen. If orthohydrogen is not removed from rapidly liquified hydrogen, without a catalyst, the heat released during its decay can boil off as much as 50% of the original liquid.

History

The unusual heat capacity of hydrogen was discovered in 1912 by Arnold Eucken.[11] The two forms of molecular hydrogen were first proposed by Werner Heisenberg and Friedrich Hund in 1927. Taking into account this theoretical framework, pure parahydrogen was first synthesized by Paul Harteck and Karl Friedrich Bonhoeffer in 1929.[12] When Heisenberg was awarded the 1932 Nobel prize in physics for the creation of quantum mechanics, this discovery of the "allotropic forms of hydrogen" was singled out as its most noteworthy application.[13] Modern isolation of pure parahydrogen has since been achieved using rapid in-vacuum deposition of millimeters thick solid parahydrogen (p–H₂) samples which are notable for their excellent optical qualities.[14]

Use in NMR

When an excess of parahydrogen is used during hydrogenation reactions (instead of the normal mixture of orthohydrogen to parahydrogen of 3:1), the resultant product exhibits hyperpolarized signals in proton NMR spectra, an effect termed PHIP (Parahydrogen Induced Polarisation) or, equivalently, PASADENA (Parahydrogen And Synthesis Allow Dramatically Enhanced Nuclear Alignment; named for first recognition of the effect by Bowers and Weitekamp of Caltech),[15] a phenomenon that has been used to study the mechanism of hydrogenation reactions.[16][17]

Signal amplification by reversible exchange (SABRE) is a technique to hyperpolarize samples without chemically modifying them. Compared to orthohydrogen or organic molecules, a much greater fraction of the hydrogen nuclei in parahydrogen align with an applied magnetic field. In SABRE, a metal center reversibly binds to both the test molecule and a parahydrogen molecule facilitating the target molecule to pick up the polarization of the parahydrogen.[18] This technique can be improved and utilized for a wide range of organic molecules by using an intermediate "relay" molecule like ammonia. The ammonia efficiently binds to the metal center and picks up the polarization from the parahydrogen. The ammonia then transfers it other molecules that don't bind as well to the metal catalyst.[19] This enhanced NMR signal allows the rapid analysis of very small amounts of material.

Deuterium

Diatomic deuterium (D₂) has nuclear spin isomers like diatomic hydrogen, but with different populations of the two forms because the deuterium nucleus (deuteron) is a boson with nuclear spin equal to one.[20] There are six possible nuclear spin wave functions which are ortho or symmetric to exchange of the two nuclei, and three which are para or antisymmetric.[20] Ortho states correspond to even rotational levels with symmetric rotational functions so that the total wavefunction is symmetric as required for the exchange of two bosons, and para states correspond to odd rotational levels.[20] The ground state (J = 0) populated at low temperature is ortho, and at standard temperature the ortho:para ratio is 2:1.[20]

Other substances with spin isomers

Other molecules and functional groups containing two hydrogen atoms, such as water and methylene, also have ortho- and para- forms (e.g. orthowater and parawater), but this is of little significance for their thermal properties.[21] Their ortho-para ratios differ from that of dihydrogen.

Molecular oxygen (O
₂) also exists in three lower-energy triplet states and one singlet state, as ground-state paramagnetic triplet oxygen and energized highly reactive diamagnetic singlet oxygen. These states arise from the spins of their unpaired electrons, not their protons or nuclei.

References

1. P. Atkins and J. de Paula, Atkins' Physical Chemistry, 8th edition (W.H.Freeman 2006), p. 451–2 ISBN 0-7167-8759-8
2. Matthews, M.J.; Petitpas, G.; Aceves, S.M. (2011). "A study of spin isomer conversion kinetics in supercritical fluid hydrogen for cryogenic fuel storage technologies". Appl. Phys. Lett. 99 (8): 081906. Bibcode:2011ApPhL..99h1906M. doi:10.1063/1.3628453.
3. Matsumoto, Mitsuru; Espenson, James H. (2005). "Kinetics of the Interconversion of Parahydrogen and Orthohydrogen Catalyzed by Paramagnetic Complex Ions". Journal of the American Chemical Society. 127 (32): 11447–11453. doi:10.1021/ja0524292. ISSN 0002-7863. PMID 16089474.
4. Aroulanda, Christie; Starovoytova, Larisa; Canet, Daniel (2007). "Longitudinal Nuclear Spin Relaxation ofOrtho- andPara-Hydrogen Dissolved in Organic Solvents". The Journal of Physical Chemistry A. 111 (42): 10615–10624. Bibcode:2007JPCA..11110615A. doi:10.1021/jp073162r. ISSN 1089-5639. PMID 17914761.
5. "Liquefaction of "Permanent" Gases" (PDF of lecture notes). 2011. Retrieved 2017-10-16.
6. Rock, Peter A., Chemical thermodynamics; principles and applications (Macmillan 1969) Table p.478 shows (N_o/N_p)H₂ = 0.002 at 20 K ISBN 1-891389-32-7
7. F. T. Wall (1974). Chemical Thermodynamics, 3rd Edition. W. H. Freeman and Company
8. "Thermophysical Properties of Fluid Systems". Webbook.nist.gov. Retrieved 2015-05-14.
9. Milenko, Yu. Ya.; Sibileva, R. M.; Strzhemechny, M. A. (1997-04-01). "Natural ortho-para conversion rate in liquid and gaseous hydrogen". Journal of Low Temperature Physics. 107 (1): 77–92. doi:10.1007/BF02396837. ISSN 1573-7357.
10. Milenko, Yu. Ya.; Sibileva, R. M.; Strzhemechny, M. A. (1997-04-01). "Natural ortho-para conversion rate in liquid and gaseous hydrogen". Journal of Low Temperature Physics. 107 (1): 77–92. doi:10.1007/BF02396837. ISSN 1573-7357.
11. A. Eucken, “Die Molekularwärme des Wasserstoffs bei tiefen Temperaturen.” Königlich Preußische Akademie der Wissenschaften (Berlin). Sitzungsberichte (1912): S. 141–151
12. Michael Polanyi and His Generation: Origins of the Social Construction of Science Mary Jo Nye, University of Chicago Press (2011) p.119 ISBN 0-226-61065-9
13. Werner Heisenberg – Facts Nobelprize.org
14. https://web.archive.org/web/20120831182954/http://www.stormingmedia.us/72/7208/A720893.html
15. Bowers, C. R.; Weitekamp, D. P. (1986). "Transformation of symmetrization order to nuclear-spin magnetization by chemical reaction and nuclear magnetic resonance" (PDF). Physical Review Letters. 57 (21): 2645–2648. Bibcode:1986PhRvL..57.2645B. doi:10.1103/physrevlett.57.2645. PMID 10033824.
16. Duckett, S. B.; Mewis (2013). Improving NMR and MRI Sensitivity With Parahydrogen. Top. Curr. Chem. Topics in Current Chemistry. 338. pp. 75–103. doi:10.1007/128_2012_388. ISBN 978-3-642-39727-1. PMID 23138689.
17. Adams, R. W.; Aguilar, J. A.; Atkinson, K. D.; Cowley, M. J.; Elliott, P. I.; Duckett, S. B.; Green, G. G.; Khazal, I. G.; López-Serrano, J; Williamson, D. C. (2009). "Reversible interactions with para-hydrogen enhance NMR sensitivity by polarization transfer" (PDF). Science. 323 (5922): 1708–11. Bibcode:2009Sci...323.1708A. doi:10.1126/science.1168877. PMID 19325111.
18. Eshuis, Nan; Aspers, Ruud L.E.G.; van Weerdenburg, Bram J.A.; Feiters, Martin C.; Rutjes, Floris P.J.T.; Wijmenga, Sybren S.; Tessari, Marco (2016). "Determination of long-range scalar 1 H– 1 H coupling constants responsible for polarization transfer in SABRE". Journal of Magnetic Resonance. 265: 59–66. Bibcode:2016JMagR.265...59E. doi:10.1016/j.jmr.2016.01.012. ISSN 1090-7807. PMID 26859865.
19. Iali, Wissam; Rayner, Peter J.; Duckett, Simon B. (2018). "Using para hydrogen to hyperpolarize amines, amides, carboxylic acids, alcohols, phosphates, and carbonates". Science Advances. 4 (1): eaao6250. Bibcode:2018SciA....4O6250I. doi:10.1126/sciadv.aao6250. ISSN 2375-2548. PMC 5756661. PMID 29326984.
20. Hollas, J. Michael (1996). Modern Spectroscopy (3rd ed.). John Wiley and Sons. p. 115. ISBN 0-471-96523-5.
21. Shinitzky, Meir; Elitzur, Avshalom C. (2006). "Ortho-para spin isomers of the protons in the methylene group". Chirality. 18 (9): 754–756. doi:10.1002/chir.20319. PMID 16856167.

Further reading

• Aline Léon, Ed. 2008, Hydrogen Technology: Mobile and Portable Applications, pp. 93–101, New York, NY:Springer Science & Business, ISBN 3-540-69925-2, see , accessed 10 May 2015.
• Tikhonov V. I., Volkov A. A. (2002). "Separation of water into its ortho and para isomers". Science. 296 (5577): 2363. doi:10.1126/science.1069513. PMID 12089435.
• Mario E. Fajardo; Simon Tam (1997). Rapid Vapor Deposition of Millimeters Thick Optically Transparent Solid Parahydrogen Samples for Matrix Isolation Spectroscopy. Edwards AFB (Propulsion Directorate West):USAF Research Lab.
• Bowers, C. R.; Weitekamp, D. P. (1986). "Transformation of symmetrization order to nuclear-spin magnetization by chemical reaction and nuclear magnetic resonance" (PDF). Phys. Rev. Lett. 57 (21): 2645–2648. Bibcode:1986PhRvL..57.2645B. doi:10.1103/physrevlett.57.2645. PMID 10033824.
• A. Farkas (1935). Orthohydrogen, parahydrogen and heavy hydrogen. The Cambridge series of physical chemistry. Cambridge, U.K.:CUP.
• Bonhoeffer KF, Harteck P (1929). "Para- and ortho hydrogen". Zeitschrift für Physikalische Chemie B. 4 (1–2): 113–141.
• Oxford Instruments, Date Unknown, "Boosting the Sensitivity of NMR Spectroscopy using Parahydrogen"