Paden–Kahan subproblems

Paden–Kahan subproblems are a set of solved geometric problems which occur frequently in inverse kinematics of common robotic manipulators.[1] Although the set of problems is not exhaustive, it may be used to simplify inverse kinematic analysis for many industrial robots.[2]

Simplification strategies

For a structure equation defined by the product of exponentials method, Paden–Kahan subproblems may be used to simplify and solve the inverse kinematics problem. Notably, the matrix exponentials are non-commutative.

Generally, subproblems are applied to solve for particular points in the inverse kinematics problem (e.g., the intersection of joint axes) in order to solve for joint angles.

Eliminating revolute joints

Simplification is accomplished by the principle that a rotation has no effect on a point lying on its axis. For example, if the point ${\textstyle p}$ is on the axis of a revolute twist ${\textstyle \xi }$, its position is unaffected by the actuation of the twist. To wit:

$${\displaystyle e^{{\widehat {\xi }}\theta }p=p}$$

Thus, for a structure equation

$${\displaystyle e^{{\widehat {\xi }}_{1}\theta _{1}}e^{{\widehat {\xi }}_{2}\theta _{2}}e^{{\widehat {\xi }}_{3}\theta _{3}}=g}$$

where ${\textstyle \xi _{1}}$, ${\textstyle \xi _{2}}$ and ${\textstyle \xi _{3}}$ are all zero-pitch twists, applying both sides of the equation to a point ${\textstyle p}$ which is on the axis of ${\textstyle \xi _{3}}$ (but not on the axes of ${\textstyle \xi _{1}}$ or ${\textstyle \xi _{2}}$) yields

$${\displaystyle e^{{\widehat {\xi }}_{1}\theta _{1}}e^{{\widehat {\xi }}_{2}\theta _{2}}e^{{\widehat {\xi }}_{3}\theta _{3}}p=gp}$$

By the cancellation of ${\textstyle \xi _{3}}$, this yields

$${\displaystyle e^{{\widehat {\xi }}_{1}\theta _{1}}e^{{\widehat {\xi }}_{2}\theta _{2}}p=gp}$$

which, if ${\textstyle \xi _{1}}$ and ${\textstyle \xi _{2}}$ intersect, may be solved by Subproblem 2.

Norm

In some cases, the problem may also be simplified by subtracting a point from both sides of the equation and taking the norm of the result.

For example, to solve

$${\displaystyle e^{{\widehat {\xi }}_{1}\theta _{1}}e^{{\widehat {\xi }}_{2}\theta _{2}}e^{{\widehat {\xi }}_{3}\theta _{3}}=g}$$

for ${\textstyle \xi _{3}}$, where ${\textstyle \xi _{1}}$ and ${\textstyle \xi _{2}}$ intersect at the point ${\textstyle q}$, both sides of the equation may be applied to a point ${\textstyle p}$ that is not on the axis of ${\textstyle \xi _{3}}$. Subtracting ${\textstyle q}$ and taking the norm of both sides yields

$${\displaystyle {\begin{aligned}\delta _{i}=\|gp-q\|=\|e^{{\widehat {\xi }}_{1}\theta _{1}}e^{{\widehat {\xi }}_{2}\theta _{2}}e^{{\widehat {\xi }}_{3}\theta _{3}}p-q\|=\|e^{{\widehat {\xi }}_{1}\theta _{1}}e^{{\widehat {\xi }}_{2}\theta _{2}}(e^{{\widehat {\xi }}_{3}\theta _{3}}p-q)\|=\|e^{{\widehat {\xi }}_{3}\theta _{3}}p-q\|\end{aligned}}}$$

This may be solved using Subproblem 3.

List of subproblems

Each subproblem is presented as an algorithm based on a geometric proof. Code to solve a given subproblem, which should be written to account for cases with multiple solutions or no solution, may be integrated into inverse kinematics algorithms for a wide range of robots.

Subproblem 1: Rotation about a single axis

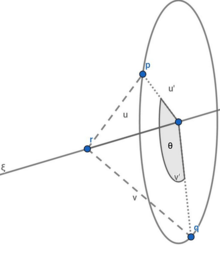An illustration of the first Paden–Kahan subproblem.

Let ${\textstyle \xi }$ be a zero-pitch twist with unit magnitude and ${\textstyle p,q\in \mathbb {R} ^{3}}$ be two points. Find ${\textstyle \theta }$ such that

$${\displaystyle e^{{\widehat {\xi }}\theta }p=q.}$$

In this subproblem, a point ${\textstyle p}$ is rotated around a given axis ${\textstyle \xi }$ such that it coincides with a second point ${\textstyle q}$.

An illustration of the projected circle in the first Paden–Kahan subproblem.

Solution

Let ${\textstyle r}$ be a point on the axis of ${\textstyle \xi }$. Define the vectors ${\textstyle u=(p-r)}$ and ${\textstyle v=(q-r)}$. Since ${\textstyle r}$ is on the axis of ${\textstyle \xi }$, ${\textstyle e^{{\widehat {\xi }}\theta }r=r.}$ Therefore, ${\textstyle e^{{\widehat {\omega }}\theta }u=v.}$

Next, the vectors ${\textstyle u'}$ and ${\textstyle v'}$ are defined to be the projections of ${\textstyle u}$ and ${\textstyle v}$ onto the plane perpendicular to the axis of ${\textstyle \xi }$. For a vector ${\textstyle \omega \in \mathbb {R} }$ in the direction of the axis of ${\textstyle \xi }$,

$${\displaystyle u'=u-\omega \omega ^{T}u}$$

and

$${\displaystyle v'=v-\omega \omega ^{T}v.}$$

In the event that ${\textstyle u'=0}$, ${\textstyle p=q}$ and both points lie on the axis of rotation. The subproblem therefore yields an infinite number of possible solutions in that case. In order for the problem to have a solution, it is necessary that the projections of ${\textstyle u}$ and ${\textstyle v}$ onto the ${\textstyle \omega }$ axis and onto the plane perpendicular to ${\textstyle \omega }$ have equal lengths. It is necessary to check, to wit, that:

$${\displaystyle \omega ^{T}u=\omega ^{T}v}$$

and that

$${\displaystyle \|u'\|=\|v'\|}$$

If these equations are satisfied, the value of the joint angle ${\textstyle \theta }$ may be found using the atan2 function:

$${\displaystyle \theta =\mathrm {atan2} (\omega ^{T}(u'\times v'),u'^{T}v').}$$

Provided that ${\textstyle u'\neq 0}$, this subproblem should yield one solution for ${\textstyle \theta }$.

Subproblem 2: Rotation about two subsequent axes

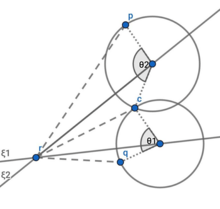Illustration of Paden–Kahan Subproblem 2. The subproblem yields two solutions in the event that the circles intersect at two points; one solution if the circles are tangential; and no solution if the circles fail to intersect.

Let ${\textstyle \xi _{1}}$ and ${\textstyle \xi _{2}}$ be two zero-pitch twists with unit magnitude and intersecting axes. Let ${\textstyle p,q\in \mathbb {R} ^{3}}$ be two points. Find ${\textstyle \theta _{1}}$ and ${\textstyle \theta _{2}}$ such that

$${\displaystyle e^{{\widehat {\xi }}_{1}\theta _{1}}e^{{\widehat {\xi }}_{2}\theta _{2}}p=q.}$$

This problem corresponds to rotating ${\textstyle p}$ around the axis of ${\textstyle \xi _{2}}$ by ${\textstyle \theta _{2}}$, then rotating it around the axis of ${\textstyle \xi _{1}}$ by ${\textstyle \theta _{1}}$, so that the final location of ${\textstyle p}$ is coincident with ${\textstyle q}$. (If the axes of ${\textstyle \xi _{1}}$ and ${\textstyle \xi _{2}}$ are coincident, then this problem reduces to Subproblem 1, admitting all solutions such that ${\textstyle \theta _{1}+\theta _{2}=\theta }$.)

Solution

Provided that the two axes are not parallel (i.e., ${\textstyle \omega _{1}\neq \omega _{2}}$), let ${\textstyle c}$ be a point such that

$${\displaystyle e^{{\widehat {\xi }}_{2}\theta _{2}}p=c=e^{-{\widehat {\xi }}_{1}\theta _{1}}q.}$$

In other words, ${\textstyle c}$ represents the point to which ${\textstyle p}$ is rotated around one axis before it is rotated around the other axis to be coincident with ${\textstyle q}$. Each individual rotation is equivalent to Subproblem 1, but it’s necessary to identify one or more valid solutions for ${\textstyle c}$ in order to solve for the rotations. Let ${\textstyle r}$ be the point of intersection of the two axes:

$${\displaystyle e^{{\widehat {\xi }}_{2}\theta _{2}}(p-r)=c-r=e^{-{\widehat {\xi }}_{1}\theta _{1}}(q-r).}$$

An illustration of Paden–Kahan subproblem 2, showing the tangential case in which the subproblem yields only one solution.

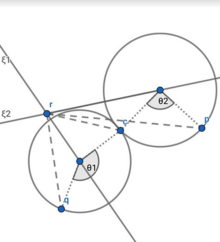
Define the vectors ${\textstyle u=(p-r)}$, ${\textstyle v=(q-r)}$ and ${\textstyle z=(c-r)}$. Therefore,

$${\displaystyle e^{{\widehat {\xi }}_{2}\theta _{2}}u=z=e^{-{\widehat {\xi }}_{1}\theta _{1}}v.}$$

This implies that ${\textstyle \omega _{2}^{T}u=\omega _{2}^{T}z}$, ${\textstyle \omega _{1}^{T}v=\omega _{1}^{T}z}$, and ${\textstyle \|u\|^{2}=\|z\|^{2}=\|v\|^{2}}$. Since ${\textstyle \omega _{1}}$, ${\textstyle \omega _{2}}$ and ${\textstyle \omega _{1}\times \omega _{2}}$ are linearly independent, ${\textstyle z}$ can be written as

$${\displaystyle z=\alpha \omega _{1}+\beta \omega _{2}+\gamma (\omega _{1}\times \omega _{2}).}$$

The values of the coefficients may be solved thus:

An illustration of Paden–Kahan subproblem 2, showing a case with two intersecting circles and therefore two solutions. Both solutions (c, c2) are highlighted.

$${\displaystyle \alpha ={\frac {(\omega _{1}^{T}\omega _{2})\omega _{2}^{T}u-\omega _{1}^{T}v}{(\omega _{1}^{T}\omega _{2})^{2}-1}}}$$

$${\displaystyle \beta ={\frac {(\omega _{1}^{T}\omega _{2})\omega _{1}^{T}v-\omega _{2}^{T}u}{(\omega _{1}^{T}\omega _{2})^{2}-1}}}$$

, and

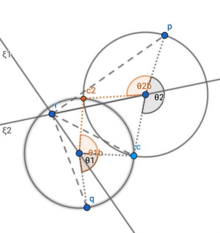
$${\displaystyle \gamma ^{2}={\frac {\|u\|^{2}-\alpha ^{2}-\beta ^{2}-2\alpha \beta \omega _{1}^{T}\omega _{2}}{\|\omega _{1}\times \omega _{2}\|^{2}.}}}$$

The subproblem yields two solutions in the event that the circles intersect at two points; one solution if the circles are tangential; and no solution if the circles fail to intersect.

Subproblem 3: Rotation to a given distance

Let ${\textstyle \xi }$ be a zero-pitch twist with unit magnitude; let ${\textstyle p,q\in \mathbb {R} ^{3}}$ be two points; and let ${\textstyle \delta }$ be a real number greater than 0. Find ${\textstyle \theta }$ such that

$${\displaystyle \|q-e^{{\widehat {\xi }}\theta }p\|=\delta .}$$

In this problem, a point ${\textstyle p}$ is rotated about an axis ${\textstyle \xi }$ until the point is a distance ${\textstyle \delta }$ from a point ${\textstyle q}$. In order for a solution to exist, the circle defined by rotating ${\textstyle p}$ around ${\textstyle \xi }$ must intersect a sphere of radius ${\textstyle \delta }$ centered at ${\textstyle q}$.

Solution

Let ${\textstyle r}$ be a point on the axis of ${\textstyle \xi }$. The vectors ${\textstyle u=(p-r)}$ and ${\textstyle v=(q-r)}$ are defined so that

$${\displaystyle \|v-e^{{\widehat {\xi }}\theta }u\|^{2}=\delta ^{2}.}$$

The projections of ${\textstyle u}$ and ${\textstyle v}$ are ${\textstyle u'=u-\omega \omega ^{T}u}$ and ${\textstyle v'=v-\omega \omega ^{T}v.}$ The “projection” of the line segment defined by ${\textstyle \delta }$ is found by subtracting the component of ${\textstyle p-q}$ in the ${\textstyle \omega }$ direction:

$${\displaystyle \delta '^{2}=\delta ^{2}-|\omega ^{T}(p-q)|^{2}.}$$

The angle ${\textstyle \theta _{0}}$ between the vectors ${\textstyle u'}$ and ${\textstyle v'}$ is found using the atan2 function:

$${\displaystyle \theta _{0}=atan2(\omega ^{T}(u'\times v'),u'^{T}v').}$$

The joint angle ${\textstyle \theta }$ is found by the formula

$${\displaystyle \theta =\theta _{0}\pm \cos ^{-1}\left({\frac {\|u'\|^{2}+\|v'\|^{2}-\delta '^{2}}{2\|u'\|\|v'\|}}\right).}$$

This subproblem may yield zero, one, or two solutions, depending on the number of points at which the circle of radius ${\textstyle \|u'\|}$ intersects the circle of radius ${\textstyle \delta '}$.

Subproblem 4: Rotation about two axes to a given distance

Let ${\textstyle \xi _{1}}$ and ${\textstyle \xi _{2}}$ be two zero-pitch twists with unit magnitude and intersecting axes. Let ${\textstyle p,q_{1},q_{2}\in \mathbb {R} ^{3}}$ be points. Find ${\textstyle \theta _{1}}$ and ${\textstyle \theta _{2}}$ such that

$${\displaystyle \|e^{{\widehat {\xi }}_{1}\theta _{1}}e^{{\widehat {\xi }}_{2}\theta _{2}}p-q_{1}\|=\delta _{1}.}$$

This problem is analogous to Subproblem 2, except that the final point is constrained by distances to two known points.

Subproblem 5: Translation to a given distance

Let ${\textstyle \xi }$ be an infinite-pitch unit magnitude twist; ${\textstyle p,q\in \mathbb {R} ^{3}}$ two points; and ${\textstyle \delta }$ a real number greater than 0. Find ${\textstyle \theta }$ such that

$${\displaystyle \|q-e^{{\widehat {\xi }}\theta }p\|=\delta .}$$

References

1. Paden, Bradley Evan (1985). "Kinematics and Control of Robot Manipulators". Ph.D. Thesis. Bibcode:1985PhDT........94P.
2. Sastry, Richard M. Murray ; Zexiang Li ; S. Shankar (1994). A mathematical introduction to robotic manipulation (PDF) (1. [Dr.] ed.). Boca Raton, Fla.: CRC Press. ISBN 9780849379819.