PISO algorithm

PISO algorithm (Pressure-Implicit with Splitting of Operators) was proposed by Issa in 1986 without iterations and with large time steps and a lesser computing effort. It is an extension of the SIMPLE algorithm used in computational fluid dynamics to solve the Navier-Stokes equations. PISO is a pressure-velocity calculation procedure for the Navier-Stokes equations developed originally for non-iterative computation of unsteady compressible flow, but it has been adapted successfully to steady-state problems.

PISO involves one predictor step and two corrector steps and is designed to satisfy mass conservation using predictor-corrector steps.

Algorithm steps

Flow chart of PISO algorithm

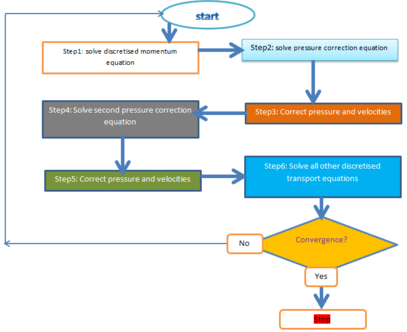
The algorithm can be summed up as follows:

1. Set the boundary conditions.
2. Solve the discretized momentum equation to compute an intermediate velocity field.
3. Compute the mass fluxes at the cells faces.
4. Solve the pressure equation.
5. Correct the mass fluxes at the cell faces.
6. Correct the velocities on the basis of the new pressure field.
7. Update the boundary conditions.
8. Repeat from 3 for the prescribed number of times.
9. Increase the time step and repeat from 1.

As already seen for the SIMPLE algorithm, the steps 4 and 5 can be repeated for a prescribed number of times to correct for non-orthogonality.

Predictor step

Guess the pressure field ${\displaystyle p^{*}}$ and get velocity field components ${\displaystyle u^{*}}$ and ${\displaystyle v^{*}}$ using discretized momentum equation. The initial guess for the pressure may or may not be correct.
Corrector step 1
Velocity component obtained from predictor step may not satisfy the continuity equation, so we define correction factors p',v',u' for the pressure field and velocity field. Solve the momentum equation by inserting correct pressure field ${\displaystyle p^{**}}$ and get the corresponding correct velocity components ${\displaystyle u^{**}}$ and ${\displaystyle v^{**}}$.

${\displaystyle p'=p^{**}-p^{*}}$

${\displaystyle v'=v^{**}-v^{*}}$
${\displaystyle u'=u^{**}-u^{*}}$
where ;
${\displaystyle p^{**},u^{**},v^{**}}$ :correct pressure field and velocity component
${\displaystyle p',u',v'}$ :correction in pressure field and correction in velocity components
${\displaystyle p^{*},u^{*},v^{*}}$ :guessed pressure field and velocity component
We define ${\displaystyle p',u',v'}$ as above. By putting the correct pressure field ${\displaystyle p^{**}}$ into the discretized momentum equation we get the correct velocity components ${\displaystyle v^{**}}$ and ${\displaystyle u^{**}}$. Once the pressure correction ${\displaystyle p'}$ is known we can find the correction components for the velocity: ${\displaystyle u'}$ and ${\displaystyle v'}$.

Corrector step 2 In piso another corrector step can be used.
${\displaystyle p^{***}=p^{**}+p''}$ ; ${\displaystyle p''=p^{*}+p'}$
${\displaystyle u^{***}=u^{**}+u''}$ ; ${\displaystyle u''=u^{*}+u'}$
${\displaystyle v^{***}=v^{**}+v''}$ ; ${\displaystyle v''=v^{*}+v'}$
where : ${\displaystyle p^{***},v^{***},u^{***}}$ are the correct pressure field and the correct velocity components, respectively
and ${\displaystyle p'',v'',u''}$ are second corrections to the pressure and velocity field.
Set ${\displaystyle p=p^{***},v=v^{***},u=u^{***}}$ where; ${\displaystyle p,v,u}$ are correct pressure and velocity field

Advantages and disadvantages

1. Generally gives more stable results and takes less CPU time but not suitable for all processes.
2. Suitable numerical schemes for solving the pressure-velocity linked equation.
3. For laminar backward facing step PISO is faster than SIMPLE but it is slower concerning flow through heated fin.
4. If momentum and scalar equation have weak or no coupling then PISO is better than SIMPLEC.

See also

• Fluid mechanics
• Computational fluid dynamics
• Algorithm
• SIMPLE algorithm
• SIMPLER algorithm
• SIMPLEC algorithm

References

1. An Introduction to Computational Fluid Dynamics The Finite Volume Method, 2/e By Versteeg ISBN 978-0131274983
2. Computational Fluid Dynamics for Engineers by Bengt Andersson, Ronnie Andersson, Love Håkansson, Mikael Mortensen, Rahman Sudiyo, Berend van Wachem ISBN 978-1-107-01895-2
3. Computational Fluid Dynamics in Fire Engineering: Theory, Modelling and Practice by Guan Heng Yeoh, Kwok Kit Yuen ISBN 978-0750685894
4. http://openfoamwiki.net/index.php/OpenFOAM_guide/The_PISO_algorithm_in_OpenFOAM
5. Computational fluid dynamics by T. J. Chung, University of Alabama in Huntsville ISBN 0 521 59416 2
6. Computational method for fluid dynamics by Joel H.Ferziger,Milovan Peric ISBN 3-540-42074-6
7. Solution of the implicitly discretized fluid flow equations by operator-splitting, Journal of Computational Physics 62 by R. Issa