Orthopole
In geometry, the orthopole of a system consisting of a triangle ABC and a line ℓ in the same plane is a point determined as follows.[1] Let A ′, B ′, C ′ be the feet of perpendiculars dropped on ℓ from A, B, C respectively. Let A ′′, B ′′, C ′′ be the feet of perpendiculars dropped from A ′, B ′, C ′ to the sides opposite A, B, C (respectively) or to those sides' extensions. Then the three lines A ′ A ′′, B ′ B ′′, C ′ C ′′, are concurrent.[2] The point at which they concur is the orthopole.
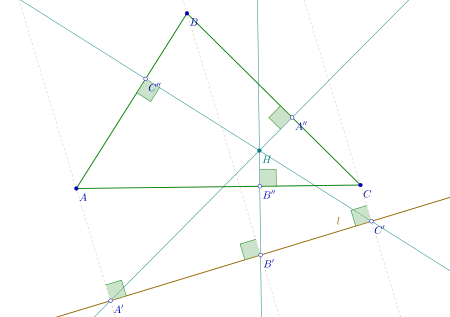
Due to their many properties,[3] orthopoles have been the subject of a large literature.[4] Some key topics are determination of the lines having a given orthopole[5]and orthopolar circles.[6]
References
- "MathWorld: Orthopole".
- https://www.jstage.jst.go.jp/article/tmj1911/27/0/27_0_77/_pdf
- "The Orthopole". 21 January 2017.
- "The Orthopole Loci of Some One-Parameter Systems of Lines Referred to a Fixed Triangle" Author(s): O. J. Ramler The American Mathematical Monthly, Vol. 37, No. 3 (Mar., 1930), pp. 130–136 Published by: Mathematical Association of America Stable URL: https://www.jstor.org/stable/2299415
- "The Projective Theory of Orthopoles", Sister Mary Cordia Karl, The American Mathematical Monthly, Vol. 39, No. 6 (June–July, 1932), pp. 327–338 Published by: Mathematical Association of America Stable URL: https://www.jstor.org/stable/2300757
- Goormaghtigh, R. (1 December 1946). "1936. The orthopole". The Mathematical Gazette. 30 (292): 293. doi:10.2307/3610737. JSTOR 3610737 – via Cambridge Core.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.