Orthogonal convex hull

In geometry, a set K ⊂ R^d is defined to be orthogonally convex if, for every line L that is parallel to one of standard basis vectors, the intersection of K with L is empty, a point, or a single segment. The term "orthogonal" refers to corresponding Cartesian basis and coordinates in Euclidean space, where different basis vectors are perpendicular, as well as corresponding lines. Unlike ordinary convex sets, an orthogonally convex set is not necessarily connected.

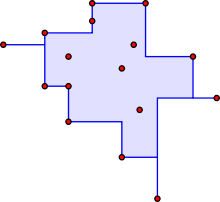
The orthogonal convex hull of a point set

The orthogonal convex hull of a set K ⊂ R^d is the intersection of all connected orthogonally convex supersets of K.

These definitions are made by analogy with the classical theory of convexity, in which K is convex if, for every line L, the intersection of K with L is empty, a point, or a single segment. Orthogonal convexity restricts the lines for which this property is required to hold, so every convex set is orthogonally convex but not vice versa. For the same reason, the orthogonal convex hull itself is a subset of the convex hull of the same point set. A point p belongs to the orthogonal convex hull of K if and only if each of the closed axis-aligned orthants having p as apex has a nonempty intersection with K.

The orthogonal convex hull is also known as the rectilinear convex hull, or, in two dimensions, the x-y convex hull.

Example

The figure shows a set of 16 points in the plane and the orthogonal convex hull of these points. As can be seen in the figure, the orthogonal convex hull is a polygon with some degenerate edges connecting extreme vertices in each coordinate direction. For a discrete point set such as this one, all orthogonal convex hull edges are horizontal or vertical. In this example, the orthogonal convex hull is connected.

Alternative definitions

A set of six points in the plane. The Classical Ortho-convex Hull is the point set it self.

The Maximal Ortho-convex Hull of the point set of the top figure. It is formed by the point set and the colored area.

A Connected Ortho-convex Hull of the point set of the top figure. It is formed by the point set, the colored area and the two ortho-convex polygonal chains.

The Functional Ortho-convex Hull of the point set of the top figure. It is formed by the point set, the colored area, and the four line segments.

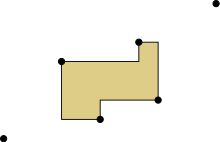
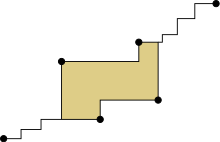
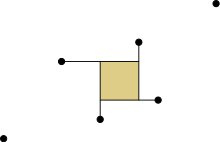
In contrast with the classical convexity where there exist several equivalent definitions of the convex hull, definitions of the orthogonal convex hull made by analogy to those of the convex hull result in different geometric objects. So far, researchers have explored the following four definitions of the orthogonal convex hull of a set ${\displaystyle K\subset \mathbb {R} ^{d}}$:

1. Maximal definition: The definition described in the introduction of this article. It is based on the Maxima of a point set.
2. Classical definition: The orthogonal convex hull of ${\displaystyle K}$ is the intersection of all orthogonally convex supersets of ${\displaystyle K}$; Ottmann, Soisalon-Soininen & Wood (1984).
3. Connected definition: The orthogonal convex hull of ${\displaystyle K}$ is the smallest connected orthogonally convex superset of ${\displaystyle K}$; Nicholl et al. (1983).
4. Functional definition: The orthogonal convex hull of ${\displaystyle K}$ is the intersection of the zero sets of all non-negative orthogonally convex functions that are ${\displaystyle 0}$ on ${\displaystyle K}$; Matoušek & Plecháč (1998).

In the figures on the right, the top figure shows a set of six points in the plane. The classical orthogonal convex hull of the point set is the point set itself. From top to bottom, the second to the fourth figures show respectively, the maximal, the connected, and the functional orthogonal convex hull of the point set. As can be seen, the orthogonal convex hull is a polygon with some degenerate "edges", namely, orthogonally convex alternating polygonal chains with interior angle ${\displaystyle 90^{\circ }}$ connecting extreme vertices.

Classical orthogonal convex hull

The classical orthogonal convex hull can be equivalently defined as the smallest orthogonally convex superset of a set ${\displaystyle K\subset \mathbb {R} ^{2}}$, by analogy to the following definition of the convex hull: the convex hull of ${\displaystyle K}$ is the smallest convex superset of ${\displaystyle K}$. The classical orthogonal convex hull might be disconnected. If a point set has no pair of points on a line parallel to one of the standard basis vectors, the classical orthogonal convex hull of such point set is equal to the point set itself.

A well known property of convex hulls is derived from the Carathéodory's theorem: A point ${\displaystyle x\in \mathbb {R} ^{d}}$ is in the interior of the convex hull of a point set ${\displaystyle K\subset \mathbb {R} ^{d}}$ if, and only if, it is already in the convex hull of ${\displaystyle d+1}$ or fewer points of ${\displaystyle K}$. This property is also valid for classical orthogonal convex hulls.

Connected orthogonal convex hull

By definition, the connected orthogonal convex hull is always connected. However, it is not unique. Consider for example a pair of points in the plane not lying on an horizontal or a vertical line. The connected orthogonal convex hull of such points is an orthogonally convex alternating polygonal chain with interior angle ${\displaystyle 90^{\circ }}$ connecting the points. Any such polygonal chain has the same length, so there are infinitely many connected orthogonal convex hulls for the point set.

For point sets in the plane, the connected orthogonal convex hull can be easily obtained from the maximal orthogonal convex hull. If the maximal orthogonal convex hull of a point set ${\displaystyle K\subset \mathbb {R} ^{2}}$ is connected, then it is equal to the connected orthogonal convex hull of ${\displaystyle K}$. If this is not the case, then there are infinitely many connected orthogonal convex hulls for ${\displaystyle K}$, and each one can be obtained by joining the connected components of the maximal orthogonal convex hull of ${\displaystyle K}$ with orthogonally convex alternating polygonal chains with interior angle ${\displaystyle 90^{\circ }}$.

Functional orthogonal convex hull

The functional orthogonal convex hull is not defined using properties of sets, but properties of functions about sets. Namely, it restricts the notion of convex function as follows. A function ${\displaystyle f:\mathbb {R} ^{d}\rightarrow \mathbb {R} }$ is called orthogonally convex if its restriction to each line parallel to a non-zero of the standard basis vectors is a convex function.

Algorithms

Several authors have studied algorithms for constructing orthogonal convex hulls: Montuno & Fournier (1982); Nicholl et al. (1983); Ottmann, Soisalon-Soininen & Wood (1984); Karlsson & Overmars (1988). By the results of these authors, the orthogonal convex hull of n points in the plane may be constructed in time O(n log n), or possibly faster using integer searching data structures for points with integer coordinates.

Related concepts

It is natural to generalize orthogonal convexity to restricted-orientation convexity, in which a set K is defined to be convex if all lines having one of a finite set of slopes must intersect K in connected subsets; see e.g. Rawlins (1987), Rawlins and Wood (1987, 1988), or Fink and Wood (1996, 1998).

In addition, the tight span of a finite metric space is closely related to the orthogonal convex hull. If a finite point set in the plane has a connected orthogonal convex hull, that hull is the tight span for the Manhattan distance on the point set. However, orthogonal hulls and tight spans differ for point sets with disconnected orthogonal hulls, or in higher-dimensional L^p spaces.

O'Rourke (1993) describes several other results about orthogonal convexity and orthogonal visibility.

References

• Biswas, Arindam; Bhowmick, Partha; Sarkar, Moumita; Bhattacharya, Bhargab B. (2012), "A Linear-time Combinatorial Algorithm to Find the Orthogonal Hull of an Object on the Digital Plane", Information Sciences, 216: 176–195, doi:10.1016/j.ins.2012.05.029.
• Fink, Eugene; Wood, Derick (1996), "Fundamentals of restricted-orientation convexity" (PDF), Information Sciences, 92 (1–4): 175–196, doi:10.1016/0020-0255(96)00056-4.
• Fink, Eugene; Wood, Derick (1998), "Generalized halfspaces in restricted-orientation convexity" (PDF), Journal of Geometry, 62 (1–2): 99–120, doi:10.1007/BF01237603.
• Karlsson, Rolf G.; Overmars, Mark H. (1988), "Scanline algorithms on a grid", BIT, 28 (2): 227–241, doi:10.1007/BF01934088.
• Matoušek, J.; Plecháč, P. (1998), "On Functional Separately Convex Hulls", Discrete & Computational Geometry, 19 (1): 105–130, doi:10.1007/PL00009331.
• Montuno, D. Y.; Fournier, A. (1982), Finding the x-y convex hull of a set of x-y polygons, Technical Report 148, University of Toronto.
• Nicholl, T. M.; Lee, D. T.; Liao, Y. Z.; Wong, C. K. (1983), "On the X-Y convex hull of a set of X-Y polygons", BIT, 23 (4): 456–471, doi:10.1007/BF01933620.
• O'Rourke, Joseph (1993), Computational Geometry in C, Cambridge University Press, pp. 107–109.
• Ottmann, T.; Soisalon-Soininen, E.; Wood, Derick (1984), "On the definition and computation of rectilinear convex hulls", Information Sciences, 33 (3): 157–171, doi:10.1016/0020-0255(84)90025-2.
• Rawlins, G. J. E. (1987), Explorations in Restricted-Orientation Geometry, Ph.D. thesis and Tech. Rep. CS-87-57, University of Waterloo.
• Rawlins, G. J. E.; Wood, Derick (1987), "Optimal computation of finitely oriented convex hulls", Information and Computation, 72 (2): 150–166, doi:10.1016/0890-5401(87)90045-9.
• Rawlins, G. J. E.; Wood, Derick (1988), "Ortho-convexity and its generalizations", in Toussaint, Godfried T. (ed.), Computational Morphology, Elsevier, pp. 137–152.