Order-6 triangular hosohedral honeycomb
In geometry, the order-6 triangular hosohedral honeycomb a regular space-filling tessellation (or honeycomb) with Schläfli symbol {2,3,6}. It has 6 triangular hosohedra {2,3} around each edge. It is a degenerate honeycomb in Euclidean space, but can be seen as a projection onto the sphere. Its vertex figure, a triangular tiling is seen on each hemisphere.
| Order-6 triangular hosohedral honeycomb | |
|---|---|
| Type | Degenerate regular honeycomb |
| Schläfli symbol | {2,3,6} |
| Coxeter diagrams | |
| Cells | {2,3} |
| Faces | {2} |
| Edge figure | {6} |
| Vertex figure | {3,6} |
| Dual | Order-2 hexagonal tiling honeycomb |
| Coxeter group | [2,3,6] |
| Properties | Regular |
Images
Stereographic projections of central spherical projection, with all edges being projected into circles. Seen below triangular tiling edges are colored into 3 parallel sets for each hemisphere.
 Centered on pole |
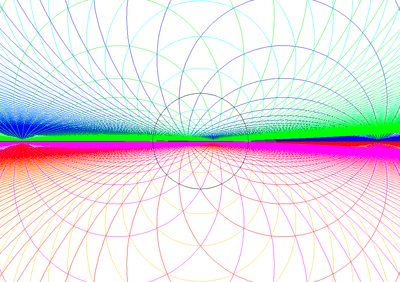 Centered on equator |
Related honeycombs
This honeycomb can be truncated as t{2,3,6} or {}×{3,6}, Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
gollark: Yep!
gollark: If you append `?source=yes` then it works.
gollark: There is. It's just not documented.
gollark: There are no users.
gollark: Oops, I may need to open stuff in WAL mode due to concurrent apioids.
See also
- Order-7 tetrahedral honeycomb
- List of regular polytopes
References
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
