Minimum deviation

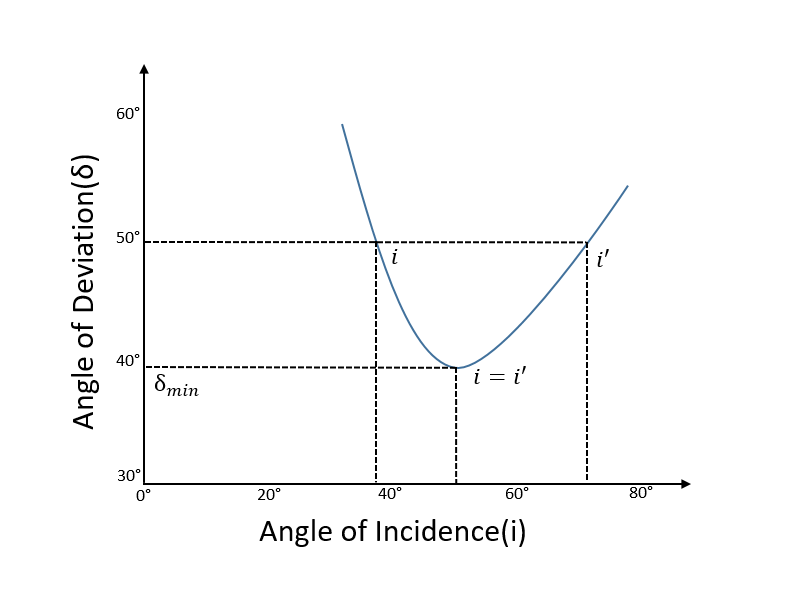
In a prism, the angle of deviation(${\displaystyle \delta }$) decreases with increase in the angle of incidence(${\displaystyle i}$) up to a particular angle. This angle of incidence where the angle of deviation in a prism is minimum is called the Minimum Deviation Position of the prism and that very deviation angle is known as the Minimum Angle of Deviation (denoted by ${\displaystyle \delta _{min}}$, ${\displaystyle D_{\lambda }}$ or ${\displaystyle D_{m}}$).

Light is deflected as it enters a material with refractive index > 1.

A ray of light is deflected twice in a prism. The sum of these deflections is the deviation angle.

When the entrance and exit angles are equal, the deviation angle of a ray passing through a prism will be minimal.

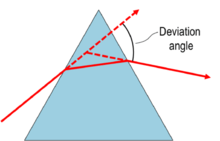
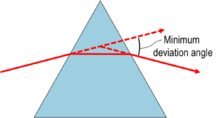
In Minimum Deviation, the refracted ray in the prism is parallel to its base. In other words, the light ray is symmetrical about the axis of symmetry of the prism.[1][2][3] Also, the angles of refractions are equal i.e. ${\displaystyle r_{1}=r_{2}}$. And, the angle of incidence and angle of emergence equal each other (${\displaystyle i=e}$). This is clearly visible in the graph in the next section.

Formula and Graph

The formula for minimum deviation can be derived by exploiting the geometry in the prism. The approach involves replacing the variables in Snell's Law in terms of the Deviation and Prism Angles by making the use of the above properties.

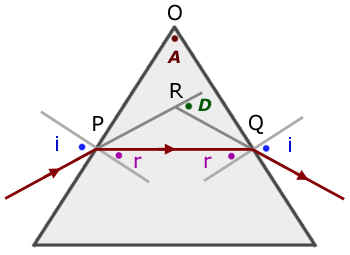
From the Angle Sum of ${\textstyle \triangle OPQ}$,

${\displaystyle A+\angle OPQ+\angle OQP=180^{\circ }}$

${\displaystyle \implies A=180^{\circ }-(90-r)-(90-r)}$

${\displaystyle \implies r={\frac {A}{2}}}$

Using the Exterior Angle Theorem in ${\textstyle \triangle PQR}$,

${\displaystyle D_{m}=\angle RPQ+\angle RQP}$

${\displaystyle \implies D_{m}=i-r+i-r}$

${\displaystyle \implies 2r+D_{m}=2i}$

${\displaystyle \implies A+D_{m}=2i}$

${\displaystyle \implies i={\frac {A+D_{m}}{2}}}$

This can also be derived by putting ${\textstyle i=e}$ in the Prism Formula: ${\textstyle i+e=A+\delta }$

From Snell's law,

${\displaystyle n_{21}={\dfrac {\sin i}{\sin r}}}$

$${\displaystyle \therefore n_{21}={\dfrac {\sin \left({\dfrac {A+D_{m}}{2}}\right)}{\sin \left({\dfrac {A}{2}}\right)}}}$$

[4][3][1][2][5]

$${\displaystyle \therefore D_{m}=2\sin ^{-1}\left(n\sin \left({\frac {A}{2}}\right)\right)-A}$$

(where ${\textstyle n}$ is the refractive index, ${\textstyle A}$ is the Angle of Prism and ${\textstyle D_{m}}$ is the Minimum Angle of Deviation.)

This is a convenient way used to measure the refractive index of a material(liquid or gas) by directing a light ray through a prism of negligible thickness at minimum deviation filled with the material or in a glass prism dipped in it.[5][3][1][6]

Question 1: The refractive index of glass is 1.5. Find the minimum angle of deviation for an equilateral prism along with the corresponding angle of incidence.

Ans.: ${\displaystyle 37^{\circ },49^{\circ }}$ Sol.: Here, ${\textstyle A=60^{\circ }}$, ${\textstyle n=1.5}$ Plugging them in the above formula, ${\textstyle {\frac {\sin \left({\frac {60+\delta }{2}}\right)}{\sin \left({\frac {60}{2}}\right)}}=1.5}$ ${\textstyle \implies {\frac {\sin \left(30+{\frac {\delta }{2}}\right)}{\sin(30)}}=1.5}$ ${\textstyle \implies \sin \left(30+{\frac {\delta }{2}}\right)=1.5\times 0.5}$ ${\textstyle \implies 30+{\frac {\delta }{2}}=\sin ^{-1}(0.75)}$ ${\textstyle \implies {\frac {\delta }{2}}=48.6-30}$ ${\textstyle \implies \delta =2\times 18.6}$ ${\textstyle \therefore \delta \approx 37^{\circ }}$ Also, ${\textstyle i={\frac {(A+\delta )}{2}}={\frac {60+2\times 18.6}{2}}\approx 49^{\circ }}$ This is also apparent in the graph below.

Question 2: If the minimum angle of deviation of a prism of refractive index 1.4 equals its refracting angle, find the angle of the prism.

Ans.: ${\displaystyle 60^{\circ }}$ Sol.: Here, ${\textstyle \delta =r}$ ${\textstyle \implies \delta ={\frac {A}{2}}}$ Using the above formula, ${\textstyle {\frac {\sin \left({\frac {A+{\frac {A}{2}}}{2}}\right)}{\sin \left({\frac {A}{2}}\right)}}=1.4}$ ${\textstyle \implies {\frac {\sin \left({\frac {3A}{4}}\right)}{\sin \left({\frac {A}{2}}\right)}}={\frac {\frac {1}{2}}{\frac {1}{\sqrt {2}}}}}$ ${\textstyle \implies {\frac {\sin \left({\frac {3A}{4}}\right)}{\sin \left({\frac {A}{2}}\right)}}={\frac {\sin 45^{\circ }}{\sin 30^{\circ }}}}$ ${\textstyle \therefore A=60^{\circ }}$

Also, the variation of the angle of deviation with an arbitrary angle of incidence can be encapsulated into a single equation by expressing ${\textstyle e}$ in terms of ${\textstyle i}$ in the Prism Formula using Snell's Law:

$${\displaystyle \delta =i-A+\sin ^{-1}\left(n\cdot \sin \left(A-\sin ^{-1}\left({\frac {\sin i}{n}}\right)\right)\right)}$$

Finding the minima of this equation will also give the same relation for minimum deviation as above.

For Thin Prism

In a thin or small angle prism, as the angles become very small, the sine of the angle nearly equals the angle itself and this yields many useful results.

${\textstyle \because D_{m}}$ and ${\textstyle A}$ are very small,

${\displaystyle \implies n\approx {\frac {\left({\frac {A+D_{m}}{2}}\right)}{\left({\frac {A}{2}}\right)}}}$

${\displaystyle \implies n={\frac {A+D_{m}}{A}}}$

${\displaystyle \implies An-A=D_{m}}$

$${\displaystyle \therefore D_{m}=A(n-1)}$$

[1][4]

Interestingly, using a similar approach with the Snell's Law and the Prism Formula for an in general thin-prism ends up in the very same result ofr the Deviation Angle.

${\textstyle \because i,e}$ and ${\textstyle r}$ are small,

${\displaystyle n\approx {\frac {i}{r_{1}}}}$ , and

${\displaystyle n\approx {\frac {e}{r_{2}}}}$

From the Prism Formula,

${\displaystyle \delta =i+e-A}$

${\displaystyle =nr_{1}+nr_{2}-A}$

${\displaystyle =n(r_{1}+r_{2})-A}$

${\displaystyle =nA-A}$

${\displaystyle =A(n-1)}$

Thus, it can be said that a Thin Prism is always in Minimum Deviation.

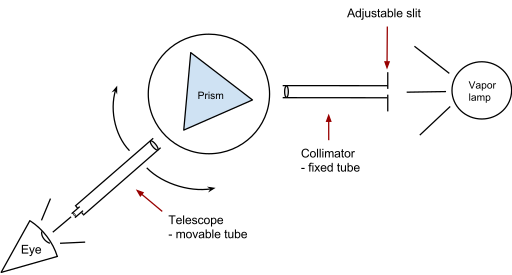
Exprimental Determination

Further information: Prism spectrometer

Minimum Deviation can be found Manually or with Spectrometer. Either the prism is kept fixed and the incidence angle is adjusted or the prism is rotated keeping the light source fixed.[7][8][9][10][11]

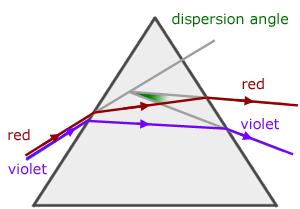
Minimum Angle of Dispersion

The Minimum Angle of Dispersion for white light is the difference in minimum deviation angle between red and violet rays of a light ray through a prism.[2]

Applications

Further information: Rainbow and Sun dog

Drawing radii to the points of interference reveals that the angles of refraction are equal, thereby proving minimum deviation.

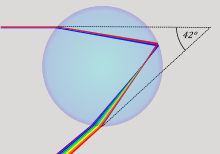
One of the factors that causes a rainbow is the bunching of light rays at the minimum deviation angle that is close to the rainbow angle(42°).[3][12]

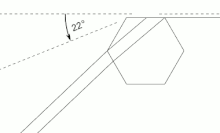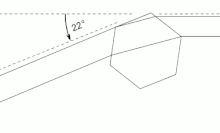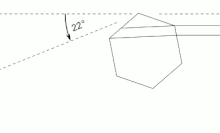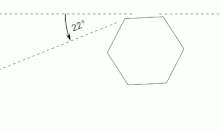
It is also responsible for phenomena like halos and sundogs, produced by the deviation of sunlight in mini prisms of hexagonal ice crystals in the air bending light with a minimum deviation of 22°.[3][13]

See Also

• Prism

• Refraction

• Geometrical optics

References/Further Reading

1. "Chapter Nine, RAY OPTICS AND OPTICAL INSTRUMENTS". Physics Part II Textbook for Class IX (PDF). NCERT. p. 331.
2. "Optics-Prism". A-Level Physics Tutor.
3. Mark A. Peterson. "Minimum Deviation by a Prism". mtholyoke. Mount Holyoke College.
4. "Refraction through Prisms". SchoolPhysics.
5. "Prism". HyperPhysics.
6. "Determination of the refractive index of the material of the prism". BrainKart.
7. "Angle of Minimum Deviation". Scribd.
8. "Theory of the Prism Spectrometer". www.ukessays.com.
9. "Experimental set up for the measurements of angle of minimum deviation using prism spectrometer". ResearchGate.
10. "Measurement of the dispersion of glass with a prism spectrometer". studylib.net.
11. "Determination of Minimum Deviation For Given Prism". BYJU'S.
12. "Rainbow". www.schoolphysics.co.uk.
13. "Halo 22°". HyperPhysics.

External Links

Minimum Deviation Part 1 and Part 2 at Khan Academy

Refraction through a Prism in NCERT Tectbook

Minimum Deviation by Prism by Mark A Peterson, Mount Holyoke College