Maximum flow problem

In optimization theory, maximum flow problems involve finding a feasible flow through a flow network that obtains the maximum possible flow rate.

pi denotes the pets, wij denotes their preference, and ri denotes the humans. Source and sink are the start and end of the flow diagram. Each edge on the network indicates the max directed flow from one node to another.

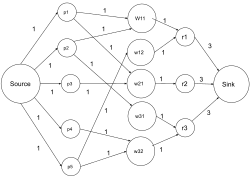
The maximum flow problem can be seen as a special case of more complex network flow problems, such as the circulation problem. The maximum value of an s-t flow (i.e., flow from source s to sink t) is equal to the minimum capacity of an s-t cut (i.e., cut severing s from t) in the network, as stated in the max-flow min-cut theorem.

History

The maximum flow problem was first formulated in 1954 by T. E. Harris and F. S. Ross as a simplified model of Soviet railway traffic flow.[1][2][3]

In 1955, Lester R. Ford, Jr. and Delbert R. Fulkerson created the first known algorithm, the Ford–Fulkerson algorithm.[4][5] In their 1955 paper,[4] Ford and Fulkerson wrote that the problem of Harris and Ross is formulated as follows (see[1] p. 5):

Consider a rail network connecting two cities by way of a number of intermediate cities, where each link of the network has a number assigned to it representing its capacity. Assuming a steady state condition, find a maximal flow from one given city to the other.

In their book Flows in Network,[5] in 1962, Ford and Fulkerson wrote:

It was posed to the authors in the spring of 1955 by T.E. Harris, who, in conjunction with General F.S. Ross (Ret.), had formulated a simplified model of railway traffic flow, and pinpointed this particular problem as the central one suggested by the model [11].

where [11] refers to the 1955 secret report Fundamentals of a Method for Evaluating Rail net Capacities by Harris and Ross[3] (see[1] p. 5).

Over the years, various improved solutions to the maximum flow problem were discovered, notably the shortest augmenting path algorithm of Edmonds and Karp and independently Dinitz; the blocking flow algorithm of Dinitz; the push-relabel algorithm of Goldberg and Tarjan; and the binary blocking flow algorithm of Goldberg and Rao. The algorithms of Sherman[6] and Kelner, Lee, Orecchia and Sidford,[7][8] respectively, find an approximately optimal maximum flow but only work in undirected graphs.

In 2013 James B. Orlin published a paper describing an ${\displaystyle O(|V||E|)}$algorithm for all values of ${\displaystyle |V|}$and ${\displaystyle |E|}$.[9]

Definition

A flow network, with source s and sink t. The numbers next to the edge are the capacities.

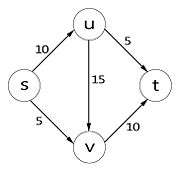
First we establish some notation:

• Let ${\displaystyle N=(V,E)}$ be a network with ${\displaystyle s,t\in V}$ being the source and the sink of ${\displaystyle N}$ respectively.
• If ${\displaystyle g}$ is function on the edges of ${\displaystyle N}$ then its value on ${\displaystyle (u,v)\in E}$ is denoted by ${\displaystyle g_{uv}}$ or ${\displaystyle g(u,v).}$

Definition. The capacity of an edge is the maximum amount of flow that can pass through an edge. Formally it is a map ${\displaystyle c:E\to \mathbb {R} ^{+}.}$

Definition. A flow is a map ${\displaystyle f:E\to \mathbb {R} ^{+}}$ that satisfies the following:

• Capacity constraint. The flow of an edge cannot exceed its capacity, in other words: ${\displaystyle f_{uv}\leq c_{uv}}$ for all ${\displaystyle (u,v)\in E.}$
• Conservation of flows. The sum of the flows entering a node must equal the sum of the flows exiting that node, except for the source and the sink. Or:

${\displaystyle \forall v\in V\setminus \{s,t\}:\quad \sum _{u:(u,v)\in E}f_{uv}=\sum _{u:(v,u)\in E}f_{vu}.}$

Remark. Flows are skew symmetric: ${\displaystyle f_{uv}=-f_{vu}}$ for all ${\displaystyle (u,v)\in E.}$

Definition. The value of flow is the amount of flow passing from the source to the sink. Formally for a flow ${\displaystyle f:E\to \mathbb {R} ^{+}}$ it is given by:

${\displaystyle |f|=\sum _{v:(s,v)\in E}f_{sv}.}$

Definition. The maximum flow problem is to route as much flow as possible from the source to the sink, in other words find the flow with maximum value.

Solutions

The following table lists algorithms for solving the maximum flow problem.

Method	Complexity	Description
Linear programming		Constraints given by the definition of a legal flow. See the linear program here.
Ford–Fulkerson algorithm	O(E max| f |)	As long as there is an open path through the residual graph, send the minimum of the residual capacities on the path. The algorithm is only guaranteed to terminate if all weights are rational. Otherwise it is possible that the algorithm will not converge to the maximum value. However, if the algorithm terminates, it is guaranteed to find the maximum value.
Edmonds–Karp algorithm	O(VE^2)	A specialization of Ford–Fulkerson, finding augmenting paths with breadth-first search.
Dinic's blocking flow algorithm	O(V^2E)	In each phase the algorithms builds a layered graph with breadth-first search on the residual graph. The maximum flow in a layered graph can be calculated in O(VE) time, and the maximum number of the phases is V-1. In networks with unit capacities, Dinic's algorithm terminates in ${\displaystyle O(\min\{V^{2/3},E^{1/2}\}E)}$ time.
MPM (Malhotra, Pramodh-Kumar and Maheshwari) algorithm[10]	O(V^3)	Only works on acyclic networks. Refer to the Original Paper.
Dinic's algorithm	O(VE log(V))	The dynamic trees data structure speeds up the maximum flow computation in the layered graph to O(V E log(V)).
General push-relabel maximum flow algorithm	O(V^2E)	The push relabel algorithm maintains a preflow, i.e. a flow function with the possibility of excess in the vertices. The algorithm runs while there is a vertex with positive excess, i.e. an active vertex in the graph. The push operation increases the flow on a residual edge, and a height function on the vertices controls which residual edges can be pushed. The height function is changed with a relabel operation. The proper definitions of these operations guarantee that the resulting flow function is a maximum flow.
Push-relabel algorithm with FIFO vertex selection rule	O(V^3)	Push-relabel algorithm variant which always selects the most recently active vertex, and performs push operations until the excess is positive or there are admissible residual edges from this vertex.
Push-relabel algorithm with dynamic trees	${\displaystyle O\left(VE\log {\frac {V^{2}}{E}}\right)}$	The algorithm builds limited size trees on the residual graph regarding to height function. These trees provide multilevel push operations.
KRT (King, Rao, Tarjan)'s algorithm[11]	${\displaystyle O(EV\log _{\frac {E}{V\log V}}V)}$
Binary blocking flow algorithm[12]	${\displaystyle O\left(E\cdot \min(V^{\frac {2}{3}},{\sqrt {E}})\cdot \log {\frac {V^{2}}{E}}\log {U}\right)}$	The value U corresponds to the maximum capacity of the network.
James B Orlin's + KRT (King, Rao, Tarjan)'s algorithm[9]	${\displaystyle O(VE)}$	Orlin's algorithm solves max-flow in O(VE) time for ${\displaystyle E\leq O(V^{{16 \over 15}-\epsilon })}$ while KRT solves it in O(VE) for ${\displaystyle E>V^{1+\epsilon }}$.

For a more extensive list, see.[13]

Integral flow theorem

The integral flow theorem states that

If each edge in a flow network has integral capacity, then there exists an integral maximal flow.

Application

Multi-source multi-sink maximum flow problem

Fig. 4.1.1. Transformation of a multi-source multi-sink maximum flow problem into a single-source single-sink maximum flow problem

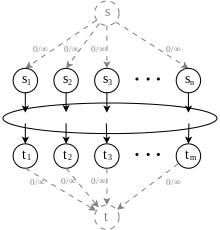
Given a network ${\displaystyle N=(V,E)}$ with a set of sources ${\displaystyle S=\{s_{1},\ldots ,s_{n}\}}$ and a set of sinks ${\displaystyle T=\{t_{1},\ldots ,t_{m}\}}$ instead of only one source and one sink, we are to find the maximum flow across ${\displaystyle N}$. We can transform the multi-source multi-sink problem into a maximum flow problem by adding a consolidated source connecting to each vertex in ${\displaystyle S}$ and a consolidated sink connected by each vertex in ${\displaystyle T}$ (also known as supersource and supersink) with infinite capacity on each edge (See Fig. 4.1.1.).

Minimum path cover in directed acyclic graph

Given a directed acyclic graph ${\displaystyle G=(V,E)}$, we are to find the minimum number of vertex-disjoint paths to cover each vertex in ${\displaystyle V}$. We can construct a bipartite graph ${\displaystyle G'=(V_{out}\cup V_{in},E')}$ from ${\displaystyle G}$, where

1. ${\displaystyle V_{out}=\{v\in V:v{\text{ has positive out-degree}}\}}$.
2. ${\displaystyle V_{in}=\{v\in V:v{\text{ has positive in-degree}}\}}$.
3. ${\displaystyle E'=\{(u,v)\in V_{out}\times V_{in}:(u,v)\in E\}}$.

Then it can be shown, via Kőnig's theorem, that ${\displaystyle G'}$ has a matching of size ${\displaystyle m}$ if and only if there exists ${\displaystyle n-m}$ vertex-disjoint paths that cover each vertex in ${\displaystyle G}$, where ${\displaystyle n}$ is the number of vertices in ${\displaystyle G}$. Therefore, the problem can be solved by finding the maximum cardinality matching in ${\displaystyle G'}$ instead.

Maximum cardinality bipartite matching

Fig. 4.3.1. Transformation of a maximum bipartite matching problem into a maximum flow problem

Given a bipartite graph ${\displaystyle G=(X\cup Y,E)}$, we are to find a maximum cardinality matching in ${\displaystyle G}$, that is a matching that contains the largest possible number of edges. This problem can be transformed into a maximum flow problem by constructing a network ${\displaystyle N=(X\cup Y\cup \{s,t\},E')}$, where

1. ${\displaystyle E'}$ contains the edges in ${\displaystyle G}$ directed from ${\displaystyle X}$ to ${\displaystyle Y}$.
2. ${\displaystyle (s,x)\in E'}$ for each ${\displaystyle x\in X}$ and ${\displaystyle (y,t)\in E'}$ for each ${\displaystyle y\in Y}$.
3. ${\displaystyle c(e)=1}$ for each ${\displaystyle e\in E'}$ (See Fig. 4.3.1).

Then the value of the maximum flow in ${\displaystyle N}$ is equal to the size of the maximum matching in ${\displaystyle G}$.

Maximum flow with vertex capacities

Fig. 4.4.1. Transformation of a maximum flow problem with vertex capacities constraint into the original maximum flow problem by node splitting

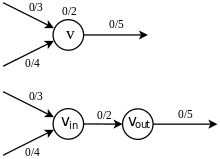
Let ${\displaystyle N=(V,E)}$ be a network. Suppose there is capacity at each node in addition to edge capacity, that is, a mapping ${\displaystyle c:V\to \mathbb {R} ^{+},}$ such that the flow ${\displaystyle f}$ has to satisfy not only the capacity constraint and the conservation of flows, but also the vertex capacity constraint

${\displaystyle \sum _{i\in V}f_{iv}\leq c(v)\qquad \forall v\in V\backslash \{s,t\}.}$

In other words, the amount of flow passing through a vertex cannot exceed its capacity. To find the maximum flow across ${\displaystyle N}$, we can transform the problem into the maximum flow problem in the original sense by expanding ${\displaystyle N}$. First, each ${\displaystyle v\in V}$ is replaced by ${\displaystyle v_{\text{in}}}$ and ${\displaystyle v_{\text{out}}}$, where ${\displaystyle v_{\text{in}}}$ is connected by edges going into ${\displaystyle v}$ and ${\displaystyle v_{\text{out}}}$ is connected to edges coming out from ${\displaystyle v}$, then assign capacity ${\displaystyle c(v)}$ to the edge connecting ${\displaystyle v_{\text{in}}}$ and ${\displaystyle v_{\text{out}}}$ (see Fig. 4.4.1). In this expanded network, the vertex capacity constraint is removed and therefore the problem can be treated as the original maximum flow problem.

Maximum number of paths from s to t

Given a directed graph ${\displaystyle G=(V,E)}$ and two vertices ${\displaystyle s}$ and ${\displaystyle t}$, we are to find the maximum number of paths from ${\displaystyle s}$ to ${\displaystyle t}$. This problem has several variants:

1. The paths must be edge-disjoint. This problem can be transformed to a maximum flow problem by constructing a network ${\displaystyle N=(V,E)}$ from ${\displaystyle G}$, with ${\displaystyle s}$ and ${\displaystyle t}$ being the source and the sink of ${\displaystyle N}$ respectively, and assigning each edge a capacity of ${\displaystyle 1}$. In this network, the maximum flow is ${\displaystyle k}$ iff there are ${\displaystyle k}$ edge-disjoint paths.

2. The paths must be independent, i.e., vertex-disjoint (except for ${\displaystyle s}$ and ${\displaystyle t}$). We can construct a network ${\displaystyle N=(V,E)}$ from ${\displaystyle G}$ with vertex capacities, where the capacities of all vertices and all edges are ${\displaystyle 1}$. Then the value of the maximum flow is equal to the maximum number of independent paths from ${\displaystyle s}$ to ${\displaystyle t}$.

3. In addition to the paths being edge-disjoint and/or vertex disjoint, the paths also have a length constraint: we count only paths whose length is exactly ${\displaystyle k}$, or at most ${\displaystyle k}$. Most variants of this problem are NP-complete, except for small values of ${\displaystyle k}$.[14]

Closure problem

Main article: Closure problem

A closure of a directed graph is a set of vertices with no outgoing edges. That is, the graph should have no edges that start within the closure and end outside the closure. The closure problem is the task of finding the maximum-weight or minimum-weight closure in a vertex-weighted directed graph. It may be solved in polynomial time using a reduction to the maximum flow problem.

Real world applications

Baseball elimination

Construction of network flow for baseball elimination problem

In the baseball elimination problem there are n teams competing in a league. At a specific stage of the league season, w_i is the number of wins and r_i is the number of games left to play for team i and r_ij is the number of games left against team j. A team is eliminated if it has no chance to finish the season in the first place. The task of the baseball elimination problem is to determine which teams are eliminated at each point during the season. Schwartz[15] proposed a method which reduces this problem to maximum network flow. In this method a network is created to determine whether team k is eliminated.

Let G = (V, E) be a network with s,t ∈ V being the source and the sink respectively. One adds a game node {i,j} with i < j to V, and connects each of them from s by an edge with capacity r_ij – which represents the number of plays between these two teams. We also add a team node for each team and connect each game node {i,j} with two team nodes i and j to ensure one of them wins. One does not need to restrict the flow value on these edges. Finally, edges are made from team node i to the sink node t and the capacity of w_k+r_k–w_i is set to prevent team i from winning more than w_k+r_k. Let S be the set of all teams participating in the league and let ${\displaystyle \scriptstyle r(S-\{k\})=\sum _{i,j\in \{S-\{k\}\},i<j}r_{ij}}$. In this method it is claimed team k is not eliminated if and only if a flow value of size r(S − {k}) exists in network G. In the mentioned article it is proved that this flow value is the maximum flow value from s to t.

Airline scheduling

In the airline industry a major problem is the scheduling of the flight crews. The airline scheduling problem can be considered as an application of extended maximum network flow. The input of this problem is a set of flights F which contains the information about where and when each flight departs and arrives. In one version of airline scheduling the goal is to produce a feasible schedule with at most k crews.

In order to solve this problem one uses a variation of the circulation problem called bounded circulation which is the generalization of network flow problems, with the added constraint of a lower bound on edge flows.

Let G = (V, E) be a network with s,t ∈ V as the source and the sink nodes. For the source and destination of every flight i, one adds two nodes to V, node s_i as the source and node d_i as the destination node of flight i. One also adds the following edges to E:

1. An edge with capacity [0, 1] between s and each s_i.
2. An edge with capacity [0, 1] between each d_i and t.
3. An edge with capacity [1, 1] between each pair of s_i and d_i.
4. An edge with capacity [0, 1] between each d_i and s_j, if source s_j is reachable with a reasonable amount of time and cost from the destination of flight i.
5. An edge with capacity [0, ∞] between s and t.

In the mentioned method, it is claimed and proved that finding a flow value of k in G between s and t is equal to finding a feasible schedule for flight set F with at most k crews.[16]

Another version of airline scheduling is finding the minimum needed crews to perform all the flights. In order to find an answer to this problem, a bipartite graph G' = (A ∪ B, E) is created where each flight has a copy in set A and set B. If the same plane can perform flight j after flight i, i∈A is connected to j∈B. A matching in G' induces a schedule for F and obviously maximum bipartite matching in this graph produces an airline schedule with minimum number of crews.[16] As it is mentioned in the Application part of this article, the maximum cardinality bipartite matching is an application of maximum flow problem.

Circulation–demand problem

There are some factories that produce goods and some villages where the goods have to be delivered. They are connected by a networks of roads with each road having a capacity c for maximum goods that can flow through it. The problem is to find if there is a circulation that satisfies the demand. This problem can be transformed into a maximum-flow problem.

1. Add a source node s and add edges from it to every factory node f_i with capacity p_i where p_i is the production rate of factory f_i.
2. Add a sink node t and add edges from all villages v_i to t with capacity d_i where d_i is the demand rate of village v_i.

Let G = (V, E) be this new network. There exists a circulation that satisfies the demand if and only if :

Maximum flow value(G) ${\displaystyle =\sum _{i\in v}d_{i}}$.

If there exists a circulation, looking at the max-flow solution would give the answer as to how much goods have to be sent on a particular road for satisfying the demands.

The problem can be extended by adding a lower bound on the flow on some edges.[17]

Image segmentation

Source image of size 8x8.

Network built from the bitmap. The source is on the left, the sink on the right. The darker an edge is, the bigger is its capacity. a_i is high when the pixel is green, b_i when the pixel is not green. The penalty p_ij are all equal.[18]

In their book, Kleinberg and Tardos present an algorithm for segmenting an image.[19] They present an algorithm to find the background and the foreground in an image. More precisely, the algorithm takes a bitmap as an input modelled as follows: a_i ≥ 0 is the likelihood that pixel i belongs to the foreground, b_i ≥ 0 in the likelihood that pixel i belongs to the background, and p_ij is the penalty if two adjacent pixels i and j are placed one in the foreground and the other in the background. The goal is to find a partition (A, B) of the set of pixels that maximize the following quantity

${\displaystyle q(A,B)=\sum _{i\in A}a_{i}+\sum _{i\in B}b_{i}-\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}}$,

Indeed, for pixels in A (considered as the foreground), we gain a_i; for all pixels in B (considered as the background), we gain b_i. On the border, between two adjacent pixels i and j, we loose p_ij. It is equivalent to minimize the quantity

${\displaystyle q'(A,B)=\sum _{i\in A}b_{i}+\sum _{i\in B}a_{i}+\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}}$

because

${\displaystyle q(A,B)=\sum _{i\in A}a_{i}+\sum _{i\in B}b_{i}-q'(A,B).}$

Minimum cut displayed on the network (triangles VS circles).

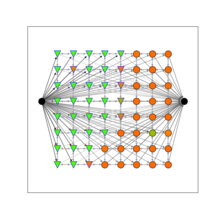
We now construct the network whose nodes are the pixel, plus a source and a sink, see Figure on the right. We connect the source to pixel i by an edge of weight a_i. We connect the pixel i to the sink by an edge of weight b_i. We connect pixel i to pixel j with weight p_ij. Now, it remains to compute a minimum cut in that network (or equivalently a maximum flow). The last figure shows a minimum cut.

Extensions

1. In the minimum-cost flow problem, each edge (u,v) also has a cost-coefficient a_uv in addition to its capacity. If the flow through the edge is f_uv, then the total cost is a_uvf_uv. It is required to find a flow of a given size d, with the smallest cost. In most variants, the cost-coefficients may be either positive or negative. There are various polynomial-time algorithms for this problem.

2. The maximum-flow problem can be augmented by disjunctive constraints: a negative disjunctive constraint says that a certain pair of edges cannot simultaneously have a nonzero flow; a positive disjunctive constraints says that, in a certain pair of edges, at least one must have a nonzero flow. With negative constraints, the problem becomes strongly NP-hard even for simple networks. With positive constraints, the problem is polynomial if fractional flows are allowed, but may be strongly NP-hard when the flows must be integral.[20]

References

1. Schrijver, A. (2002). "On the history of the transportation and maximum flow problems". Mathematical Programming. 91 (3): 437–445. CiteSeerX 10.1.1.23.5134. doi:10.1007/s101070100259.
2. Gass, Saul I.; Assad, Arjang A. (2005). "Mathematical, algorithmic and professional developments of operations research from 1951 to 1956". An Annotated Timeline of Operations Research. International Series in Operations Research & Management Science. 75. pp. 79–110. doi:10.1007/0-387-25837-X_5. ISBN 978-1-4020-8116-3.
3. Harris, T. E.; Ross, F. S. (1955). "Fundamentals of a Method for Evaluating Rail Net Capacities" (PDF). Research Memorandum.
4. Ford, L. R.; Fulkerson, D. R. (1956). "Maximal flow through a network". Canadian Journal of Mathematics. 8: 399–404. doi:10.4153/CJM-1956-045-5.
5. Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
6. Sherman, Jonah (2013). "Nearly Maximum Flows in Nearly Linear Time". Proceedings of the 54th Annual IEEE Symposium on Foundations of Computer Science. pp. 263–269. arXiv:1304.2077. doi:10.1109/FOCS.2013.36. ISBN 978-0-7695-5135-7.
7. Kelner, J. A.; Lee, Y. T.; Orecchia, L.; Sidford, A. (2014). "An Almost-Linear-Time Algorithm for Approximate Max Flow in Undirected Graphs, and its Multicommodity Generalizations" (PDF). Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms. p. 217. arXiv:1304.2338. doi:10.1137/1.9781611973402.16. ISBN 978-1-61197-338-9. Archived from the original (PDF) on 2016-03-03.
8. Knight, Helen (7 January 2014). "New algorithm can dramatically streamline solutions to the 'max flow' problem". MIT News. Retrieved 8 January 2014.
9. Orlin, James B. (2013). Max flows in O(nm) time, or better. STOC '13 Proceedings of the Forty-fifth Annual ACM Symposium on Theory of Computing. pp. 765–774. CiteSeerX 10.1.1.259.5759. doi:10.1145/2488608.2488705. ISBN 9781450320290.
10. Malhotra, V.M.; Kumar, M.Pramodh; Maheshwari, S.N. (1978). "An ${\displaystyle O(|V|^{3})}$ algorithm for finding maximum flows in networks" (PDF). Information Processing Letters. 7 (6): 277–278. doi:10.1016/0020-0190(78)90016-9.
11. King, V.; Rao, S.; Tarjan, R. (1994). "A Faster Deterministic Maximum Flow Algorithm". Journal of Algorithms. 17 (3): 447–474. doi:10.1006/jagm.1994.1044.
12. Goldberg, A. V.; Rao, S. (1998). "Beyond the flow decomposition barrier". Journal of the ACM. 45 (5): 783. doi:10.1145/290179.290181.
13. Goldberg, A. V.; Tarjan, R. E. (1988). "A new approach to the maximum-flow problem". Journal of the ACM. 35 (4): 921. doi:10.1145/48014.61051.
14. Itai, A.; Perl, Y.; Shiloach, Y. (1982). "The complexity of finding maximum disjoint paths with length constraints". Networks. 12 (3): 277–286. doi:10.1002/net.3230120306. ISSN 1097-0037.
15. Schwartz, B. L. (1966). "Possible Winners in Partially Completed Tournaments". SIAM Review. 8 (3): 302–308. doi:10.1137/1008062. JSTOR 2028206.
16. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein (2001). "26. Maximum Flow". Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill. pp. 643–668. ISBN 978-0-262-03293-3.CS1 maint: multiple names: authors list (link)
17. Carl Kingsford. "Max-flow extensions: circulations with demands" (PDF).
18. "Project imagesegmentationwithmaxflow, that contains the source code to produce these illustrations". GitLab. Retrieved 2019-12-22.
19. "Algorithm Design". www.pearson.com. Retrieved 2019-12-21.
20. Schauer, Joachim; Pferschy, Ulrich (2013-07-01). "The maximum flow problem with disjunctive constraints". Journal of Combinatorial Optimization. 26 (1): 109–119. CiteSeerX 10.1.1.414.4496. doi:10.1007/s10878-011-9438-7. ISSN 1382-6905.

Further reading

• Joseph Cheriyan and Kurt Mehlhorn (1999). "An analysis of the highest-level selection rule in the preflow-push max-flow algorithm". Information Processing Letters. 69 (5): 239–242. CiteSeerX 10.1.1.42.8563. doi:10.1016/S0020-0190(99)00019-8.
• Daniel D. Sleator and Robert E. Tarjan (1983). "A data structure for dynamic trees" (PDF). Journal of Computer and System Sciences. 26 (3): 362–391. doi:10.1016/0022-0000(83)90006-5. ISSN 0022-0000.
• Eugene Lawler (2001). "4. Network Flows". Combinatorial Optimization: Networks and Matroids. Dover. pp. 109–177. ISBN 978-0-486-41453-9.