Marginal efficiency of capital

The marginal efficiency of capital (MEC) is that rate of discount which would equate the price of a fixed capital asset with its present discounted value of expected income.

The term “marginal efficiency of capital” was introduced by John Maynard Keynes in his General Theory, and defined as “the rate of discount which would make the present value of the series of annuities given by the returns expected from the capital asset during its life just equal its supply price”.[1]

The MEC is the net rate of return that is expected from the purchase of additional capital. It is calculated as the profit that a firm is expected to earn considering the cost of inputs and the depreciation of capital. It is influenced by expectations about future input costs and demand. The MEC and capital outlays are the elements that a firm takes into account when deciding about an investment project.

The MEC needs to be higher than the rate of interest, r, for investment to take place. This is because the present value PV of future returns to capital needs to be higher than the cost of capital, Ck. These variables can be expressed as follows:

  • where n is the number of years during which the capital will be productive, and Ri is the net return in year i;
  • where Ck is the upfront capital outlays; this equation defines the MEC.

Hence, for investment to take place, it is necessary that PV > Ck; that is, MEC > r. As a consequence, an inverse relationship between the rate of interest and investment is found (i.e.: a higher rate of interest generates less investment).

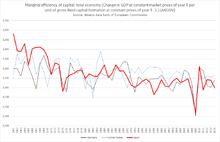
With the European Commission according to its data bank "AMECO" (Annual Macro-Economic Data) the marginal efficiency of capital is defined as "Change in GDP at constant market prices of year T per unit of gross fixed capital formation at constant prices of year T-.5 [that is, lagged by half a year].[2]

Marginal efficiency of capital as defined in the Ameco data bank of the European Commission for FRG, USA and Japan.

See also

References
  1. Keynes, John Maynard; The General Theory of Employment, Interest, and Money (1936), p 135.
  2. "Marginal Efficiency of Capital" in Ameco


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.