Maas–Hoffman model

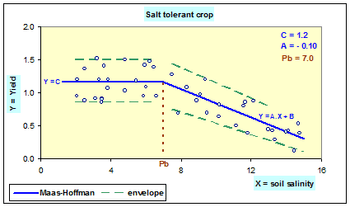
The Maas–Hoffman model is a mathematical tool to characterize the relation between crop production and soil salinity. It describes the crop response by a broken line of which the first part is horizontal and the second is sloping downward.[1] The breakpoint (Pb) or threshold is also called tolerance because up to that point the yield is unaffected by the salinity, so the salt is tolerated, while at greater salinity values the crops are affected negatively and the yield goes down.

Maas–Hoffman model fitted to a data set by regression analysis. The soil salinity on the x-axis is represented by electric conductivity (ECe). In this example the crop has a salt tolerance (threshold) of ECe = Pb = 7 dS/m beyond which the yield diminishes.

Mathematics

Mathematically the two lines are represented by the equations:

Y = C                [X < Pb]
Y = AX + B       [X > Pb]

where Y = crop production or yield, C = maximum yield, X = soil salinity, A = slope (regression coefficient) of the descending line, and B = regression constant of that line.

In the example of the figure: C = 1.2, A = —0.10, Pb = 7.0

The value of Pb is to be found by regression analysis and optimization so that the goodness of fit of the data to the model is maximum.

The Maas–Hoffman model is used in crop tolerance to seawater.

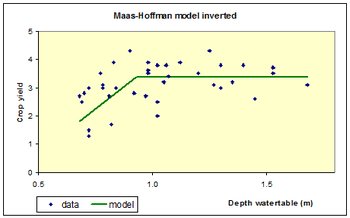
Inverted Maas-Hoffman model for the relation between crop yield and depth of the watertable

Inverted model

For growth factors, like the depth of the watertable, that affect crop production negatively at low values while there is no effect at high values, the inverted Maas–Hoffman model can be used.

gollark: No, I solved that one ages ago, it's easy.
gollark: Oh dear. I have encountered a horrible dilemma.
gollark: I see.
gollark: Relative addresses (?) everywhere?
gollark: How does position independent code work anyway?

See also

References
  1. Maas EV, Hoffman GJ, 1977. Crop salt tolerance-current assessment. Journal of the Irrigation and Drainage Division, American Society of Civil Engineers 103: 115-134.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.