MCS algorithm

Multilevel Coordinate Search (MCS) is an efficient algorithm for bound constrained global optimization using function values only.

Figure 1: MCS algorithm (without local search) applied to the two-dimensional Rosenbrock function. The global minimum ${\displaystyle f_{min}=0}$ is located at ${\displaystyle (x,y)=(1,1)}$. MCS identifies a position with ${\displaystyle f\approx 0.002}$ within 21 function evaluations. After additional 21 evaluations the optimal value is not improved and the algorithm terminates. Observe dense clustering of samples around potential minima - this effect can be reduced significantly by employing local searches appropriately.

To do so, the n-dimensional search space is represented by a set of non-intersecting hypercubes (boxes). The boxes are then iteratively split along an axis plane according to the value of the function at a representative point of the box (and its neighbours) and the box's size. These two splitting criteria combine to form a global search by splitting large boxes and a local search by splitting areas for which the function value is good.

Additionally, a local search combining a (multi-dimensional) quadratic interpolant of the function and line searches can be used to augment performance of the algorithm (MCS with local search); in this case the plain MCS is used to provide the starting (initial) points. The information provided by local searches (namely local minima of the objective function) is then fed back to the optimizer and influences the splitting criteria, resulting in reduced sample clustering around local minima and faster convergence.

Simplified workflow

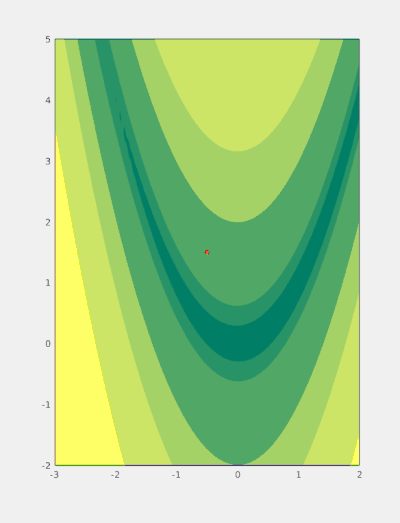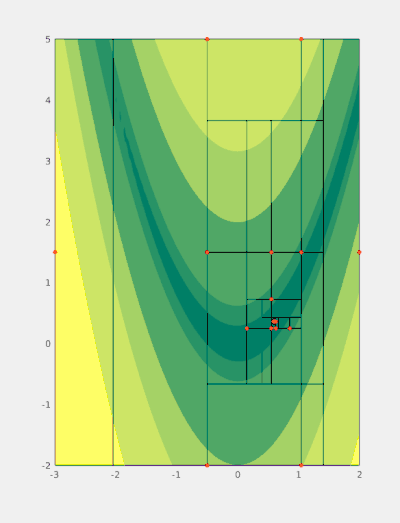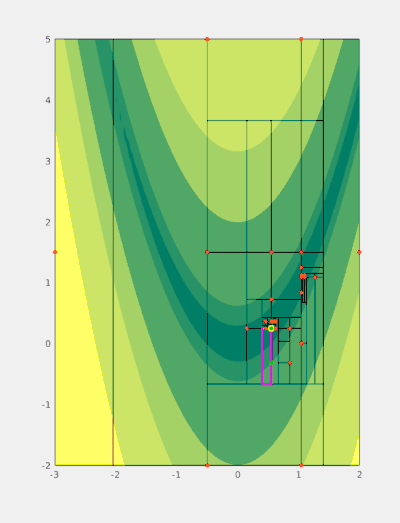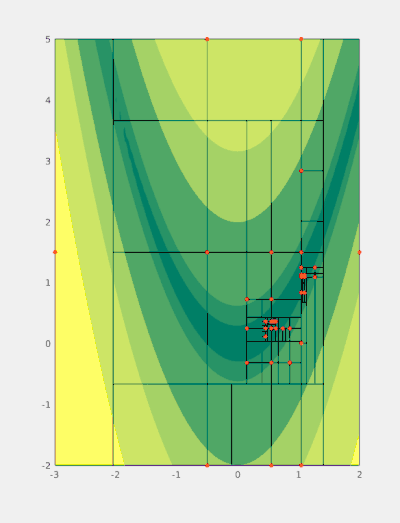
The basic workflow is presented in figure 1. Generally, each step can be characterized by three stages:

1. Identify a potential candidate for splitting (magenta, thick).
2. Identify the optimal splitting direction and the expected optimal position of splitting points (green).
3. Evaluate the objective function at splitting points not considered previously. Generate new boxes (magenta, thin) based on the values of the objective function at splitting (green) points.

At every step at least one splitting point (yellow) is a known function sample (red) hence the objective is never evaluated there again.

In order to determine if a box will be split two separate splitting criteria are used. The first one, splitting by rank, ensures that large boxes that have not been split too often will be split eventually. If it applies then the splitting point can be determined a priori. The second one, splitting by expected gain, employs a local one-dimensional quadratic model (surrogate) along a single coordinate. In this case the splitting point is defined as the minimum of the surrogate and the box is split only if the interpolant value there is lower than the current best sampled function value.

Convergence

The algorithm is guaranteed to converge to the global minimum in the long run (i.e. when the number of function evaluations and the search depth are arbitrarily large) if the objective function is continuous in the neighbourhood of the global minimizer. This follows from the fact that any box will become arbitrarily small eventually, hence the spacing between samples tends to zero as the number of function evaluations tends to infinity.

Recursive implementation

MCS was designed to be implemented in an efficient recursive way with the aid of trees. With this approach the amount of memory required is independent of problem dimensionality since the sampling points are not stored explicitly. Instead, just a single coordinate of each sample is saved and the remaining coordinates can be recovered by tracing the history of a box back to the root (initial box). This method was suggested by the authors and used in their original implementation.

When implemented carefully this also allows for avoiding repeated function evaluations. More precisely, if a sampling point is placed along the boundary of two adjacent boxes then this information can often be extracted through backtracing the point's history for a small number of steps. Consequently, new subboxes can be generated without evaluating the (potentially expensive) objective function. This scenario is visualised in figure 1 whenever a green (but not yellow) and a red point coincide e.g. when the box with corners around ${\displaystyle (-0.5,0.5)}$ and ${\displaystyle (1.0,3.5)}$ is split.

References

External links

• Homepage of the algorithm
• Performance of the algorithm relative to others