Lorraine Foster
Lorraine Lois Foster (December 25, 1938, Culver City, California) is an American mathematician. In 1964 she became the first woman to receive a Ph.D. in mathematics from California Institute of Technology.[1] Her thesis advisor at Caltech was Olga Taussky-Todd.[2]
Lorraine L. Foster | |
|---|---|
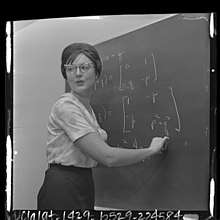 Dr. Foster in 1964. (Photo from the Los Angeles Times Photographic Collection, UCLA Library Digital Collections) | |
| Born | December 25, 1938 |
| Citizenship | American |
| Education | B.A. 1960, Occidental College; Ph.D. 1964, California Institute of Technology |
| Occupation | Mathematician |
| Employer | California State University, Northridge |
Born Lorraine Lois Turnbull, she attended Occidental College where she majored in physics. She was admitted to Caltech after receiving a Woodrow Wilson Foundation fellowship. In 1964 she joined the faculty of California State University, Northridge. She works in number theory and the theory of mathematical symmetry.
Selected bibliography
- Foster, L. (1966). On the characteristic roots of the product of certain rational integral matrices of order two. Pacific Journal of Mathematics, 18(1), 97–110. http://doi.org/10.2140/pjm.1966.18.97
- Brenner, J. L., & Foster, L. L. (1982). Exponential diophantine equations. Pacific Journal of Mathematics, 101(2), 263–301.
- Alex, L. J., & Foster, L. L. (1983). On diophantine equations of the form $1 + 2^a = p^b q^c + 2^d p^e q^f$. Rocky Mountain Journal of Mathematics, 13(2), 321–332. http://doi.org/10.1216/RMJ-1983-13-2-321
- Alex, L. J., & Foster, L. L. (1985). On the Diophantine equation $1 + p^a = 2 + 2^b + 2^c p^d$. Rocky Mountain Journal of Mathematics, 15(3), 739–762. http://doi.org/10.1216/RMJ-1985-15-3-739
- L. Forster (1989). Finite Symmetry Groups in Three Dimensions, CSUN Instructional Media Center, Jan. 1989 (video, 27 minutes).
- L. Foster (1990). Archimedean and Archimedean Dual Polyhedra, CSUN Instructional Media Center, Feb. 1990 (video, 47 minutes). https://www.worldcat.org/title/archimedean-and-archimedean-dual-polyhedra/oclc/63936926&referer=brief_results
- Foster, L. L. (1990). On the symmetry group of the dodecahedron. Mathematics Magazine, 63, 106–107.
- Foster, L. L. (1991). Convex Polyhedral Models for the Finite Three-Dimensional Isometry Groups. The Mathematical Heritage of CF Gauss, pp 267-281.
- L. Foster (1991). The Alhambra Past and Present—a Geometer’s Odyssey Part 1, CSUN Instructional Media Center, December 1991 (video, 40 minutes).
- L. Foster (1991). The Alhambra Past and Present—a Geometer’s Odyssey Part 2, CSUN Instructional Media Center, December 1991 (video, 40 minutes). https://www.worldcat.org/title/alhambra-past-and-present-a-geometers-odyssey-parts-1-and-2/oclc/28680624?loc=94043&tab=holdings&start_holding=7
- Foster, L. L. (1991). Convex polyhedral models for the finite three-dimensional isometry groups. In G. M. Rassias (Ed.), The Mathematical Heritage of C F Gauss (pp. 267–281). Singapore: World Scientific.
- L. Foster (1992). Regular-Faced Polyhedra—an Introduction, CSUN Instructional Media Center, Dec. 1992 (video, 47 minutes)
- Alex, L. J., & Foster, L. L. (1992). On the Diophantine equation $\bf 1+x+y=z$. Rocky Mountain Journal of Mathematics, 22(1), 11–62. http://doi.org/10.1216/rmjm/1181072793
- Alex, L. J., & Foster, L. L. (1995). On the Diophantine equation $w+x+y=z$, with $wxyz=2\sp r3\sp s5\sp t$. Rev. Mat. Univ. Complut. Madrid, 8(1), 13–48.
gollark: However, I just did it by immediately typing all possible words before the computer had registered any time.
gollark: Advanced!
gollark: If you do not have backups, you're asking for spontaneous disk implosion to delete all your datas.
gollark: Of your data.
gollark: You should really have backups anyway.
References
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.