List of shapes with known packing constant

The packing constant of a geometric body is the largest average density achieved by packing arrangements of congruent copies of the body. For most bodies the value of the packing constant is unknown.[1] The following is a list of bodies in Euclidean spaces whose packing constant is known.[1] Fejes Tóth proved that in the plane, a point symmetric body has a packing constant that is equal to its translative packing constant and its lattice packing constant.[2] Therefore, any such body for which the lattice packing constant was previously known, such as any ellipse, consequently has a known packing constant. In addition to these bodies, the packing constants of hyperspheres in 8 and 24 dimensions are almost exactly known.[3]

Image	Description	Dimension	Packing constant	Comments
	All shapes that tile space	all	1	By definition
	Circle, Ellipse	2	π/√12 ≈ 0.906900	Proof attributed to Thue[4]
	Smoothed octagon	2	${\displaystyle \eta _{so}={\frac {8-4{\sqrt {2}}-\ln {2}}{2{\sqrt {2}}-1}}\approx 0.902414\,.}$	Reinhardt[5]
	All 2-fold symmetric convex polygons	2		Linear-time (in number of vertices) algorithm given by Mount and Ruth Silverman[6]
	Sphere	3	π/√18 ≈ 0.7404805	See Kepler conjecture
	Bi-infinite cylinder	3	π/√12 ≈ 0.906900	Bezdek and Kuperberg[7]
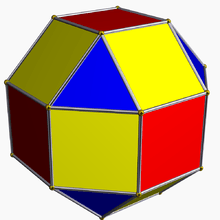	All shapes contained in a rhombic dodecahedron whose inscribed sphere is contained in the shape	3	Fraction of the volume of the rhombic dodecahedron filled by the shape	Corollary of Kepler conjecture. Examples pictured: rhombicuboctahedron and rhombic enneacontahedron.
	Hypersphere	8	${\displaystyle {\frac {({\frac {\pi }{2}})^{4}}{4!}}\approx 0.2536695}$	See Hypersphere packing[8][9]
	Hypersphere	24	${\displaystyle {\frac {({\frac {\pi }{2}})^{12}}{12!}}\approx 0.000000471087}$	See Hypersphere packing

References

1. Bezdek, András; Kuperberg, Włodzimierz (2010). "Dense packing of space with various convex solids". arXiv:1008.2398v1 [math.MG].
2. Fejes Tóth, László (1950). "Some packing and covering theorems". Acta Sci. Math. Szeged. 12.
3. Cohn, Henry; Kumar, Abhinav (2009). "Optimality and uniqueness of the Leech lattice among lattices". Annals of Mathematics. 170 (3): 1003–1050. arXiv:math.MG/0403263. doi:10.4007/annals.2009.170.1003.
4. Chang, Hai-Chau; Wang, Lih-Chung (2010). "A Simple Proof of Thue's Theorem on Circle Packing". arXiv:1009.4322v1 [math.MG].
5. Reinhardt, Karl (1934). "Über die dichteste gitterförmige Lagerung kongruente Bereiche in der Ebene und eine besondere Art konvexer Kurven". Abh. Math. Sem. Univ. Hamburg. 10: 216–230. doi:10.1007/bf02940676.
6. Mount, David M.; Silverman, Ruth (1990). "Packing and covering the plane with translates of a convex polygon". Journal of Algorithms. 11 (4): 564–580. doi:10.1016/0196-6774(90)90010-C.
7. Bezdek, András; Kuperberg, Włodzimierz (1990). "Maximum density space packing with congruent circular cylinders of infinite length". Mathematika. 37: 74–80. doi:10.1112/s0025579300012808.
8. Klarreich, Erica (March 30, 2016), "Sphere Packing Solved in Higher Dimensions", Quanta Magazine
9. Viazovska, Maryna (2016). "The sphere packing problem in dimension 8". Annals of Mathematics. 185 (3): 991–1015. arXiv:1603.04246. doi:10.4007/annals.2017.185.3.7.