Legendre rational functions
In mathematics the Legendre rational functions are a sequence of orthogonal functions on [0, ∞). They are obtained by composing the Cayley transform with Legendre polynomials.
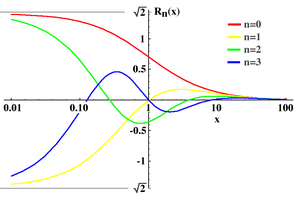
Plot of the Legendre rational functions for n=0,1,2 and 3 for x between 0.01 and 100.
A rational Legendre function of degree n is defined as:
where is a Legendre polynomial. These functions are eigenfunctions of the singular Sturm-Liouville problem:
with eigenvalues
Properties
Many properties can be derived from the properties of the Legendre polynomials of the first kind. Other properties are unique to the functions themselves.
Recursion
and
Limiting behavior
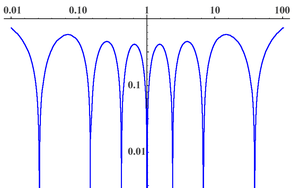
Plot of the seventh order (n=7) Legendre rational function multiplied by 1+x for x between 0.01 and 100. Note that there are n zeroes arranged symmetrically about x=1 and if x0 is a zero, then 1/x0 is a zero as well. These properties hold for all orders.
It can be shown that
and
Particular values
gollark: I decided to try and see if this was some sort of apiaristic issue with I/O and not actual markdown handling directly, but no! Even a minimal program which just reads the file and markdownizes it takes 4 seconds!
gollark: How could it *possibly* be this slow?
gollark: ... how is it *slower* now?
gollark: One issue complains about `htmlEntityToUtf8` being awful and bee, so I've tried removing that.
gollark: There's a library for that, but I need to add custom parsing bits.
References
Zhong-Qing, Wang; Ben-Yu, Guo (2005). "A mixed spectral method for incompressible viscous fluid flow in an infinite strip". Mat. Apl. Comput. 24 (3). doi:10.1590/S0101-82052005000300002.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.