Lawvere–Tierney topology
In mathematics, a Lawvere–Tierney topology is an analog of a Grothendieck topology for an arbitrary topos, used to construct a topos of sheaves. A Lawvere–Tierney topology is also sometimes also called a local operator or coverage or topology or geometric modality. They were introduced by William Lawvere (1971) and Myles Tierney.
Definition
If E is a topos, then a topology on E is a morphism j from the subobject classifier Ω to Ω such that j preserves truth (), preserves intersections (), and is idempotent ().
j-closure
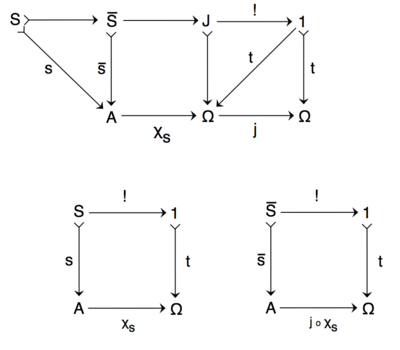
Given a subobject of an object A with classifier , then the composition defines another subobject of A such that s is a subobject of , and is said to be the j-closure of s.
Some theorems related to j-closure are (for some subobjects s and w of A):
- inflationary property:
- idempotence:
- preservation of intersections:
- preservation of order:
- stability under pullback: .
Examples
Grothendieck topologies on a small category C are essentially the same as Lawvere–Tierney topologies on the topos of presheaves of sets over C.
References
- Lawvere, F. W. (1971), "Quantifiers and sheaves", Actes du Congrès International des Mathématiciens (Nice, 1970) (PDF), 1, Paris: Gauthier-Villars, pp. 329–334, MR 0430021
- Mac Lane, Saunders; Moerdijk, Ieke (1994), Sheaves in geometry and logic. A first introduction to topos theory, Universitext, New York: Springer-Verlag. Corrected reprint of the 1992 edition.
- McLarty, Colin (1995) [1992], Elementary Categories, Elementary Toposes, Oxford Logic Guides, New York: Oxford University Press, p. 196