Late-life mortality deceleration

In gerontology, late-life mortality deceleration is the disputed theory that hazard rate increases at a decreasing rate in late life rather than increasing exponentially as in the Gompertz law.

US period life table for 2003, showing considerable acceleration rather than deceleration.

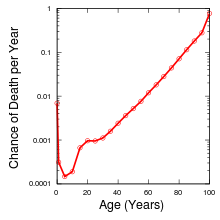
Late-life mortality deceleration is a well-established phenomenon in insects,[1] which often spend much of their lives in a constant hazard rate region, but it is much more controversial in mammals.[2] Rodent studies have found varying conclusions, with some finding short-term periods of mortality deceleration in mice, others not finding such. Baboon studies show no mortality deceleration.

An analogous deceleration occurs in the failure rate of manufactured products; this analogy is elaborated in the reliability theory of aging and longevity.[1][3]

Late-life mortality deceleration was first proposed as occurring in human aging in Gompertz (1825) (which also introduced the Gompertz law), and observed as occurring in humans in Greenwood & Irwin (1939), and has since become one of the pillars of the biodemography of human longevity – see history; here "late life" is typically "after 85 years of age". However, a recent paper, Gavrilov & Gavrilova (2011), concludes that mortality deceleration is negligible up to the age of 106 in the population studied (beyond this point, reliable data were unavailable) and that the Gompertz law is a good fit, with previous observations of deceleration being spurious, with various causes, including bad data and methodological problems – see criticism.

The primary reference for this article is Gavrilov & Gavrilova (2011), which provides a detailed historical overview and discussion, together with current criticism.

Phenomena

Three related terms are used in this context:

Late-life mortality deceleration

Hazard rate increasing at a decreasing rate (rather than increasing log-linearly as in the Gompertz law).

Mortality leveling-off

More strongly, hazard rate eventually stops increasing (or rather, asymptotes towards a limit), and then proceeds at a constant rate (or rather, approaches a constant rate), yielding (slightly sub-) exponential decay, as in radioactive decay.

Late-life mortality plateau

This is used synonymously with "mortality leveling-off", or rather to refer to the region where hazard rate is approximately constant.

History

A brief historical review is given in Gavrilov & Gavrilova (2011, 2. Mortality at Advanced Ages: A Historical Review (pp. 433–435)); a detailed survey is given in Olshansky (1998).

Late-life mortality deceleration was first proposed as occurring in human aging, in Gompertz (1825), which also introduced the Gompertz law.[4] It was observed and quantified in Greenwood & Irwin (1939), and reproduced in many later studies. Greenwood and Irwin wrote:

"the increase of mortality rate with age advances at a slackening rate, that nearly all, perhaps all, methods of graduation of the type of Gompertz’s formula over-state senile mortality"[5]

"the possibility that with advancing age the rate of mortality asymptotes to a finite value"[5]

"the limiting values of q_x [one-year probability of death] are 0.439 for women and 0.544 for men"[6]

Following these studies, late-life mortality deceleration became one of the pillars of the theory of biodemography of human longevity, and models have incorporated it. It has been criticized at times, and recently has been very seriously criticized; see below.

Criticism

Statistical studies of extreme longevity are difficult for a number of factors. Firstly, because few people live to very old ages, a very large population is required for such studies, ideally all born and living in similar conditions (same country, same birth year). In small countries, a single birth year cohort is insufficiently numerous for statistics, and thus multiple years are often used. Secondly, due to the great ages, accurate records of persons living over 100 years require records dating from the late 19th or early 20th century, when such record-keeping was often not high-quality; further, there is a tendency to exaggerate one's age, which distorts data. Thirdly, granularity is an issue – ideally exact day of birth and death would be used; using only year of birth and death introduces granularity, which adds bias (as discussed below).

Gavrilov & Gavrilova (2011) examined single birth-year cohorts from the United States Death Master File, using the method of extinct generations, and found that the effect disappeared if various distorting factors were removed. Specifically, they conclude that mortality deceleration is negligible up to the age of 106 in the population studied (beyond this point, reliable data were unavailable) and that the Gompertz law is a good fit, with previous observations of deceleration being spurious, with various causes, discussed below.

Why was mortality deceleration observed?

Given that mortality deceleration in humans had been observed in various studies, but disappeared on the careful analysis (of single-year cohorts in the US) in Gavrilov & Gavrilova (2011), it is natural to ask what causes this discrepancy – why was mortality deceleration observed?

Gavrilov & Gavrilova (2011) propose several causes; notable, in each instance when such a factor is corrected or diminished, the fit with the Gompertz law becomes better.

Data quality:

• Age exaggeration

  There is at times a tendency for old people to exaggerate their ages; this reduces apparent mortality.

Technical:

• Use of probability of death (over an discrete interval of time, usually one year), rather than the hazard rate (force of mortality; instantaneous rate)

  For those of sufficient age, this appears to divide the death rate by their age, because as people age that one year becomes a smaller and smaller fraction of their life.

  Probabilities of death can be reconstructed using the Sacher formula, if necessary.

• Use of biased estimators of theoretical hazard rate

  Since the Gompertz law is log-linear, working on a semi-log scale and taking the central difference quotient of the logarithm yields an unbiased and maximum likelihood estimator (assuming intervals and change in the hazard rate are small), but other methods, such as the "actuarial estimate", yield bias (especially due to concavity of an exponential function on a linear scale).

Methodology:

• Mixing together several birth cohorts with different mortality levels
• Using cross-sectional instead of cohort data
• Crude assumptions, such as uniformity of death over a time interval

  For example, if hazard rate is high, significantly more deaths should be expected in the first month of the period than the last month (since fewer people survive to the end); assuming that deaths occur evenly throughout the period or in the middle of the period overstates length of life.

Causes

Several causes are proposed for late-life mortality:[1]

• Population heterogeneity (first proposed in Beard (1959)), is by far the most common explanation of mortality deceleration. Even if individual hazard rate follows a Gompertz law, if the population is heterogeneous, the population hazard rate may exhibit late-life deceleration.
• Redundancy exhaustion – in the reliability theory of aging, an organism's redundancy (reserves) are exhausted at extremely old ages, so every random hit results in death. In more detailed accounts, this only holds in relatively simple organisms – in more complex organisms with various subsystems, deceleration is less present or entirely absent.
• Less risky behavior and more sheltered environment for older people.[7]
• Various evolutionary explanations.

Modeling

Late-life mortality deceleration can be modeled via modifications of the Gompertz law, using various logistic models.

Relevance

The rates of late-life mortality are important for pensions. For example, the mortality rates in late life (after age 85) are of particular interest for the baby boom generation, which will reach this age starting in 2030, and for pensions funding calculations.

Late-life mortality rates are of basic importance for understanding aging, both for organisms generally and for humans specifically.

Citations

1. Gavrilov & Gavrilova 2011, p. 434.
2. Gavrilov & Gavrilova 2011, pp. 433–434.
3. Economos 1979.
4. Gavrilov & Gavrilova 2011, p. 433.
5. Greenwood & Irwin 1939, p. 14.
6. Greenwood & Irwin 1939, p. 21.
7. Greenwood & Irwin 1939.

References

• Beard, R. E. (1959). "Note on Some Mathematical Mortality Models". In Wolstenholme, G.E.W.; O'Connor, M. O. (eds.). The Lifespan of Animals, Volume 5: Colloquia on Ageing. Boston: Little, Brown. pp. 302–311. ISBN 978-0-470-71494-2.CS1 maint: ref=harv (link)
• Economos, A. C. (1979). "A non-Gompertzian paradigm for mortality kinetics of metazoan animals and failure kinetics of manufactured products". AGE. Springer. 2 (3): 74–76. doi:10.1007/bf02432250. ISSN 0161-9152.CS1 maint: ref=harv (link)
• Gavrilov, Leonid A.; Gavrilova, Natalia S. (2011). "Mortality Measurement at Advanced Ages: A Study of the Social Security Administration Death Master File" (PDF). North American Actuarial Journal: 432–447. doi:10.1080/10920277.2011.10597629, Press Release: Mortality Grossly Underestimated at Older Ages, New Study FindsCS1 maint: ref=harv (link)
• Gompertz, B. (1825). "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies". Philosophical Transactions of the Royal Society of London. 115: 513–585. doi:10.1098/rstl.1825.0026.CS1 maint: ref=harv (link)
• Greenwood, M.; Irwin, J. O. (1939). "The biostatistics of senility". Human Biology. Wayne State University Press. 11 (1): 1–23. ISSN 0018-7143. JSTOR 41447403.CS1 maint: ref=harv (link)
• Olshansky, S. J. (1998). "On the Biodemography of Aging: A Review Essay". Population and Development Review. 24 (2): 381–393. doi:10.2307/2807981. JSTOR 2807981.CS1 maint: ref=harv (link)

External links

• Late-Life Mortality Deceleration, Mortality Levelling-off, Mortality Plateaus, Population Heterogeneity (models) – references