Lamb–Oseen vortex

In fluid dynamics, the Lamb–Oseen vortex models a line vortex that decays due to viscosity. This vortex is named after Horace Lamb and Carl Wilhelm Oseen[1].[2]

Vector plot of the Lamb–Oseen vortex velocity field.

Evolution of a Lamb–Oseen vortex in air in real time. Free-floating test particles reveal the velocity and vorticity pattern. (scale: image is 20 cm wide)

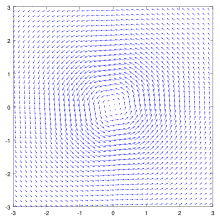
Mathematical description

Oseen looked for a solution for the Navier-Stokes equations in cylindrical coordinates ${\displaystyle (r,\theta ,z)}$ with velocity components ${\displaystyle (v_{r},v_{\theta },v_{z})}$ of the form

${\displaystyle v_{r}=0,\quad v_{\theta }={\frac {\Gamma }{2\pi r}}g(r,t),\quad v_{z}=0.}$

where ${\displaystyle \Gamma }$ is the circulation of the vortex core. This lead Navier-Stokes equations to reduce to

${\displaystyle {\frac {\partial g}{\partial t}}=\nu \left({\frac {\partial ^{2}g}{\partial r^{2}}}-{\frac {1}{r}}{\frac {\partial g}{\partial r}}\right)}$

which when is subjected to the conditions that is regular at ${\displaystyle r=0}$ and becomes unity as ${\displaystyle r\rightarrow \infty }$, leads to[3]

${\displaystyle g(r,t)=1-\mathrm {e} ^{-r^{2}/4\nu t},}$

where ${\displaystyle \nu }$ is the kinematic viscosity of the fluid. At ${\displaystyle t=0}$, we have a potential vortex with concentrated vorticity at the ${\displaystyle z}$ axis; and this vorticity diffuses away as time passes.

The only non-zero vorticity component is in the ${\displaystyle z}$ direction, given by

${\displaystyle \omega _{z}(r,t)={\frac {\Gamma }{4\pi \nu t}}\mathrm {e} ^{-r^{2}/4\nu t}.}$

The pressure field simply ensures the vortex rotates in the circumferential direction, providing the centripetal force

${\displaystyle {\partial p \over \partial r}=\rho {v^{2} \over r},}$

where ρ is the constant density[4]

Generalized Oseen vortex

The generalized Oseen vortex may obtained by looking for solutions of the form

${\displaystyle v_{r}=-\gamma (t)r,\quad v_{\theta }={\frac {\Gamma }{2\pi r}}g(r,t),\quad v_{z}=2\gamma (t)z}$

that leads to the equation

${\displaystyle {\frac {\partial g}{\partial t}}-\gamma r{\frac {\partial g}{\partial r}}=\nu \left({\frac {\partial ^{2}g}{\partial r^{2}}}-{\frac {1}{r}}{\frac {\partial g}{\partial r}}\right).}$

Self-similar solution exists for the coordinate ${\displaystyle \eta =r/\phi (t)}$, provided ${\displaystyle \phi \phi '+\gamma \phi ^{2}=a}$, where ${\displaystyle a}$ is a constant, in which case ${\displaystyle g=1-\mathrm {e} ^{-a\eta ^{2}/2\nu }}$. The solution for ${\displaystyle \phi (t)}$ may be written according to Rott (1958)[5] as

${\displaystyle \phi ^{2}=2a\exp \left(-2\int _{0}^{t}\gamma (s)\,\mathrm {d} s\right)\int _{c}^{t}\exp \left(2\int _{0}^{u}\gamma (s)\,\mathrm {d} s\right)\,\mathrm {d} u,}$

where ${\displaystyle c}$ is an arbitrary constant. For ${\displaystyle \gamma =0}$, the classical Lamb-Oseen vortex is recovered. The case ${\displaystyle \gamma =k}$ corresponds to the axisymmetric stagnation point flow, where ${\displaystyle k}$ is a constant. When ${\displaystyle c=-\infty }$, ${\displaystyle \phi ^{2}=a/k}$, a Burgers vortex is a obtained. For arbitrary ${\displaystyle c}$, the solution becomes ${\displaystyle \phi ^{2}=a(1+\beta \mathrm {e} ^{-2kt})/k}$, where ${\displaystyle \beta }$ is an arbitrary constant. As ${\displaystyle t\rightarrow \infty }$, Burgers vortex is recovered.

References

1. Oseen, C. W. (1912). Uber die Wirbelbewegung in einer reibenden Flussigkeit. Ark. Mat. Astro. Fys., 7, 14-26.
2. Saffman, P. G.; Ablowitz, Mark J.; J. Hinch, E.; Ockendon, J. R.; Olver, Peter J. (1992). Vortex dynamics. Cambridge: Cambridge University Press. ISBN 0-521-47739-5. p. 253.
3. Drazin, P. G., & Riley, N. (2006). The Navier-Stokes equations: a classification of flows and exact solutions (No. 334). Cambridge University Press.
4. G.K. Batchelor (1967). An Introduction to Fluid Dynamics. Cambridge University Press.
5. Rott, N. (1958). On the viscous core of a line vortex. Zeitschrift für angewandte Mathematik und Physik ZAMP, 9(5-6), 543-553.