Laman graph
In graph theory, the Laman graphs are a family of sparse graphs describing the minimally rigid systems of rods and joints in the plane. Formally, a Laman graph is a graph on n vertices such that, for all k, every k-vertex subgraph has at most 2k − 3 edges, and such that the whole graph has exactly 2n − 3 edges. Laman graphs are named after Gerard Laman, of the University of Amsterdam, who in 1970 used them to characterize rigid planar structures.[1] This characterization, however, had already been discovered in 1927 by Hilda Geiringer.[2]
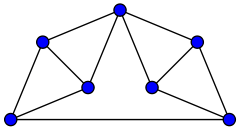
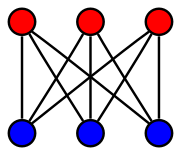
Rigidity
Laman graphs arise in rigidity theory: if one places the vertices of a Laman graph in the Euclidean plane, in general position, there will in general be no simultaneous motion of all the points, other than Euclidean congruences, that preserves the lengths of all the graph edges. A graph is rigid in this sense if and only if it has a Laman subgraph that spans all of its vertices. Thus, the Laman graphs are exactly the minimally rigid graphs, and they form the bases of the two-dimensional rigidity matroids.
If n points in the plane are given, then there are 2n degrees of freedom in their placement (each point has two independent coordinates), but a rigid graph has only three degrees of freedom (the position of a single one of its vertices and the rotation of the remaining graph around that vertex). Intuitively, adding an edge of fixed length to a graph reduces its number of degrees of freedom by one, so the 2n − 3 edges in a Laman graph reduce the 2n degrees of freedom of the initial point placement to the three degrees of freedom of a rigid graph. However, not every graph with 2n − 3 edges is rigid; the condition in the definition of a Laman graph that no subgraph can have too many edges ensures that each edge contributes to reducing the overall number of degrees of freedom, and is not wasted within a subgraph that is already itself rigid due to its other edges.
Planarity
A pointed pseudotriangulation is a planar straight-line drawing of a graph, with the properties that the outer face is convex, that every bounded face is a pseudotriangle, a polygon with only three convex vertices, and that the edges incident to every vertex span an angle of less than 180 degrees. The graphs that can be drawn as pointed pseudotriangulations are exactly the planar Laman graphs.[3] However, Laman graphs have planar embeddings that are not pseudotriangulations, and there are Laman graphs that are not planar, such as the utility graph K3,3.
Sparsity
Lee & Streinu (2008) and Streinu & Theran (2009) define a graph as being -sparse if every nonempty subgraph with vertices has at most edges, and -tight if it is -sparse and has exactly edges. Thus, in their notation, the Laman graphs are exactly the (2,3)-tight graphs, and the subgraphs of the Laman graphs are exactly the (2,3)-sparse graphs. The same notation can be used to describe other important families of sparse graphs, including trees, pseudoforests, and graphs of bounded arboricity.[4][5]
Based on this characterization, it is possible to recognize n-vertex Laman graphs in time O(n2), by simulating a "pebble game" that begins with a graph with n vertices and no edges, with two pebbles placed on each vertex, and performs a sequence of the following two kinds of steps to create all of the edges of the graph:
- Create a new directed edge connecting any two vertices that both have two pebbles, and remove one pebble from the start vertex of the new edge.
- If an edge points from a vertex u with at most one pebble to another vertex v with at least one pebble, move a pebble from v to u and reverse the edge.
If these operations can be used to construct an orientation of the given graph, then it is necessarily (2,3)-sparse, and vice versa. However, faster algorithms are possible, running in time , based on testing whether doubling one edge of the given graph results in a multigraph that is (2,2)-tight (equivalently, whether it can be decomposed into two edge-disjoint spanning trees) and then using this decomposition to check whether the given graph is a Laman graph.[6]
Henneberg construction
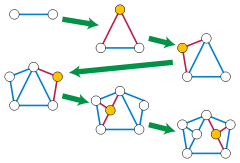
Before Laman's and Geiringer's work, Lebrecht Henneberg characterized the two-dimensional minimally rigid graphs (that is, the Laman graphs) in a different way.[7] Henneberg showed that the minimally rigid graphs on two or more vertices are exactly the graphs that can be obtained, starting from a single edge, by a sequence of operations of the following two types:
- Add a new vertex to the graph, together with edges connecting it to two previously existing vertices.
- Subdivide an edge of the graph, and add an edge connecting the newly formed vertex to a third previously existing vertex.
A sequence of these operations that forms a given graph is known as a Henneberg construction of the graph. For instance, the complete bipartite graph K3,3 may be formed using the first operation to form a triangle and then applying the second operation to subdivide each edge of the triangle and connect each subdivision point with the opposite triangle vertex.
References
- Laman, G. (1970), "On graphs and the rigidity of plane skeletal structures", J. Engineering Mathematics, 4 (4): 331–340, Bibcode:1970JEnMa...4..331L, doi:10.1007/BF01534980, MR 0269535.
- Pollaczek‐Geiringer, Hilda (1927), "Über die Gliederung ebener Fachwerke", Zeitschrift für Angewandte Mathematik und Mechanik, 7 (1): 58–72.
- Haas, Ruth; Orden, David; Rote, Günter; Santos, Francisco; Servatius, Brigitte; Servatius, Herman; Souvaine, Diane; Streinu, Ileana; Whiteley, Walter (2005), "Planar minimally rigid graphs and pseudo-triangulations", Computational Geometry Theory and Applications, 31 (1–2): 31–61, arXiv:math/0307347, doi:10.1016/j.comgeo.2004.07.003, MR 2131802.
- Lee, Audrey; Streinu, Ileana (2008), "Pebble game algorithms and sparse graphs", Discrete Mathematics, 308 (8): 1425–1437, arXiv:math/0702129, doi:10.1016/j.disc.2007.07.104, MR 2392060.
- Streinu, I.; Theran, L. (2009), "Sparse hypergraphs and pebble game algorithms", European Journal of Combinatorics, 30 (8): 1944–1964, arXiv:math/0703921, doi:10.1016/j.ejc.2008.12.018.
- Daescu, O.; Kurdia, A. (2009), "Towards an optimal algorithm for recognizing Laman graphs", Proc. 42nd Hawaii International Conference on System Sciences (HICSS '09), IEEE, pp. 1–10, arXiv:0801.2404, doi:10.1109/HICSS.2009.470.
- Henneberg, L. (1911), Die graphische Statik der starren Systeme, Leipzig