Knee of a curve

In mathematics, a knee of a curve (or elbow of a curve) is a point where the curve visibly bends, specifically from high slope to low slope (flat or close to flat), or in the other direction. This is particularly used in optimization, where a knee point is the optimum point for some decision, for example when there is an increasing function and a trade-off between the benefit (vertical y axis) and the cost (horizontal x axis): the knee is where the benefit is no longer increasing rapidly, and is no longer worth the cost of further increases – a cutoff point of diminishing returns.

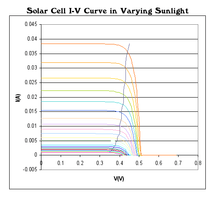
Explained variance. The "elbow" is indicated by the red circle. The number of clusters chosen should therefore be 4.
Photovoltaic solar cell I-V curves where a line intersects the knee of the curves where the maximum power transfer point is located.

In heuristic use, the term may be used informally, and a knee point identified visually, but in more formal use an explicit objective function is used, and depends on the particular optimization problem. A knee may also be defined purely geometrically, in terms of the curvature or the second derivative.

Definitions

The knee of a curve can be defined as a vertex of the graph. This corresponds with the graphical intuition (it is where the curvature has a maximum), but depends on the choice of scale.

The term "knee" as applied to curves dates at least to the 1910s,[1] and is found more commonly by the 1940s,[2] being common enough to draw criticism.[3][4] The unabridged Webster's Dictionary (1971 edition) gives definition 3h of knee as:[5]

an abrupt change in direction in a curve (as on a graph); esp one approaching a right angle in shape.

Criticism

Graphical notions of a "knee" of a curve, based on curvature, are criticized due to their dependence on the coordinate scale: different choices of scale result in different points being the "knee". This criticism dates at least to the 1940s, being found in Worthing & Geffner (1943, Preface), who criticize:[4]

references to the significance of a so-called knee of a curve when the location of the knee was a function of the chosen coordinate scales

Applications
gollark: Okay, never mind, the slice there is fine, I did it wrong in *another* thing which somehow worked.
gollark: (Although the slice there is a bit wrong and I don't know why it works anyway)
gollark: I came up with the algorithm and decided it was very cool and immediately needed implementing.
gollark: Possibly not if you can't do imports either.
gollark: Okay, you would need to do pointfree stuff, but I believe it's *doable*.

References
  1. Terrell, John Alan (1913). An Experimental Investigation of a New System for Automatically Regulating the Voltage of an Alternating Current Circuit. Rensselaer Polytechnic Institute. p. 10. ... enables one to tell how near the “knee” of the curve the iron is ...
  2. NACA Wartime Report. L. National Advisory Committee for Aeronautics. 1943. p. 21. ... the knee of the curve lies in the region of the critical load ...
  3. Worthing & Geffner 1943, Preface.
  4. Kiokemeister, Fred L. (1949). An Analysis of Functions Describing Experimental Data. Psychophysical Research. p. 5.
  5. Thomas & Sheldon 1999, p. 18.
  • Worthing, J.; Geffner, A. G. (1943). Treatment of Experimental Data.
  • Thomas, Clayton; Sheldon, Bob (1999). "The "Knee of a Curve"— Useful Clue but Incomplete Support". Military Operations Research. 4 (2): 17–24. JSTOR 43940795.CS1 maint: ref=harv (link)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.