Knaster–Kuratowski fan

In topology, a branch of mathematics, the Knaster–Kuratowski fan (named after Polish mathematicians Bronisław Knaster and Kazimierz Kuratowski) is a specific connected topological space with the property that the removal of a single point makes it totally disconnected. It is also known as Cantor's leaky tent or Cantor's teepee (after Georg Cantor), depending on the presence or absence of the apex.

The Knaster-Kuratowski fan, or "Cantor's teepee"

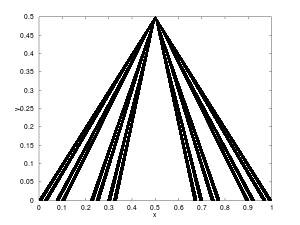
Let ${\displaystyle C}$ be the Cantor set, let ${\displaystyle p}$ be the point ${\displaystyle ({\tfrac {1}{2}},{\tfrac {1}{2}})\in \mathbb {R} ^{2}}$, and let ${\displaystyle L(c)}$, for ${\displaystyle c\in C}$, denote the line segment connecting ${\displaystyle (c,0)}$ to ${\displaystyle p}$. If ${\displaystyle c\in C}$ is an endpoint of an interval deleted in the Cantor set, let ${\displaystyle X_{c}=\{(x,y)\in L(c):y\in \mathbb {Q} \}}$; for all other points in ${\displaystyle C}$ let ${\displaystyle X_{c}=\{(x,y)\in L(c):y\notin \mathbb {Q} \}}$; the Knaster–Kuratowski fan is defined as ${\displaystyle \bigcup _{c\in C}X_{c}}$ equipped with the subspace topology inherited from the standard topology on ${\displaystyle \mathbb {R} ^{2}}$.

The fan itself is connected, but becomes totally disconnected upon the removal of ${\displaystyle p}$.

See also

• Antoine's necklace

References

• Knaster, B.; Kuratowski, C. (1921), "Sur les ensembles connexes" (PDF), Fundamenta Mathematicae, 2 (1): 206–255
• Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-486-68735-3, MR 0507446

External links