Kinetic heap

A Kinetic Heap is a kinetic data structure, obtained by the kinetization of a heap. It is designed to store elements (keys associated with priorities) where the priority is changing as a continuous function of time. As a type of kinetic priority queue, it maintains the maximum priority element stored in it. The kinetic heap data structure works by storing the elements as a tree that satisfies the following heap property – if $B$ is a child node of $A$ , then the priority of the element in $A$ must be higher than the priority of the element in $B$ . This heap property is enforced using certificates along every edge so, like other kinetic data structures, a kinetic heap also contains a priority queue (the event queue) to maintain certificate failure times.

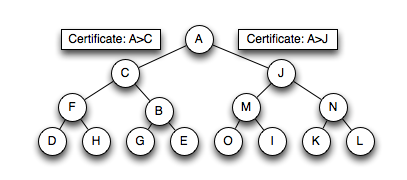
Implementation and operations

A regular heap can be kinetized by augmenting with a certificate [ $A > B$ ] for every pair of nodes $A$ , $B$ such that $B$ is a child node of $A$ . If the value stored at a node $X$ is a function $f X (t)$ of time, then this certificate is only valid while $f A (t) > f B (t)$ . Thus, the failure of this certificate must be scheduled in the event queue at a time $t$ such that $f A (t) > f B (t)$ .

All certificate failures are scheduled on the "event queue", which is assumed to be an efficient priority queue whose operations take $O(log n)$ time.

Dealing with certificate failures

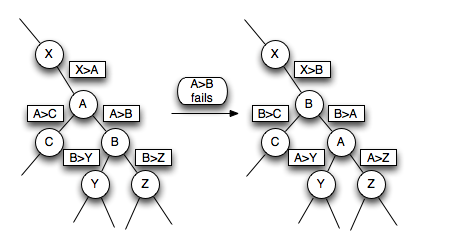
When a certificate [ $A > B$ ] fails, the data structure must swap $A$ and $B$ in the heap, and update the certificates that each of them was present in.

For example, if $B$ (call its child nodes $Y,Z$ ) was a child node of $A$ (call its child nodes $B,C$ and its parent node $X$ ), and the certificate [ $A > B$ ] fails, then the data structure must swap $B$ and $A$ , then replace the old certificates (and the corresponding scheduled events) [ $A > B$ ], [ $A < X$ ], [ $A > C$ ], [ $B > Y$ ], [ $B > Z$ ] with new certificates [ $B > A$ ], [ $B < X$ ], [ $B > C$ ], [ $A > Y$ ] and [ $A > Z$ ].

Thus, assuming non-degeneracy of the events (no two events happen at the same time), only a constant number of events need to be de-scheduled and re-scheduled even in the worst case.

Operations

A kinetic heap supports the following operations:

$create-heap (h)$ : create an empty kinetic heap $h$
$find-max (h, t)$ (or find-min): – return the $max$ (or $min$ for a $min-heap$ ) value stored in the heap $h$ at the current virtual time $t$ .
$insert (X, f X, t)$ : – insert a key $X$ into the kinetic heap at the current virtual time $t$ , whose value changes as a continuous function $f X (t)$ of time $t$ . The insertion is done as in a normal heap in $O(log n)$ time, but $O(log n)$ certificates might need to be changed as a result, so the total time for rescheduling certificate failures is $O(log 2 n)$
$delete (X, t)$ – delete a key $X$ at the current virtual time $t$ . The deletion is done as in a normal heap in $O(log n)$ time, but $O(log n)$ certificates might need to be changed as a result, so the total time for rescheduling certificate failures is $O(log 2 n)$ .

Performance

Kinetic heaps perform well according to the four metrics (responsiveness, locality, compactness and efficiency) of kinetic data structure quality defined by Basch et al.[1] The analysis of the first three qualities is straightforward:

Responsiveness: A kinetic heap is responsive, since each certificate failure causes the concerned keys to be swapped and leads to only few certificates being replaced in the worst case.
Locality: Each node is present in one certificate each along with its parent node and two child nodes (if present), meaning that each node can be involved in a total of three scheduled events in the worst case, thus kinetic heaps are local.
Compactness: Each edge in the heap corresponds to exactly one scheduled event, therefore the number of scheduled events is exactly $n -1$ where $n$ is the number of nodes in the kinetic heap. Thus, kinetic heaps are compact.

Analysis of efficiency

The efficiency of a kinetic heap in the general case is largely unknown.[1][2][3] However, in the special case of affine motion $f(t) = a t + b$ of the priorities, kinetic heaps are known to be very efficient.[2]

Affine motion, no insertions or deletions

In this special case, the maximum number of events processed by a kinetic heap can be shown to be exactly the number of edges in the transitive closure of the tree structure of the heap, which is $O(n log n)$ for a tree of height $O(log n)$ .[2]

Affine motion, with insertions and deletions

If $n$ insertions and deletions are made on a kinetic heap that starts empty, the maximum number of events processed is $O(n{\sqrt {n\log n}}).$ [4] However, this bound is not believed to be tight,[2] and the only known lower bound is $\Omega (n\log n)$ .[4]

Variants

This article deals with "simple" kinetic heaps as described above, but other variants have been developed for specialized applications,[5] such as:

Fibonacci kinetic heap
Incremental kinetic heap

Other heap-like kinetic priority queues are:

gollark: Oh, good idea, I didn't think of that, there's no actual reason they can't just use a mutable reference.

gollark: So every recursive invocation of it creates a new hashmap. This is really not ideal.

gollark: See, the main pattern matching function which matches (and binds variables in) patterns returns an option of a hashmap of bindings.

gollark: I'm relatively sure that wouldn't work.

gollark: Well, it applies reduction rules from the reduction rulesets.

References

Basch, J., Guibas, L. J., Hershberger, J (1997). "Data structures for mobile data". Proceedings of the eighth annual ACM-SIAM symposium on Discrete algorithms. SODA. Society for Industrial and Applied Mathematics. pp. 747–756. Retrieved May 17, 2012.CS1 maint: multiple names: authors list (link)
da Fonseca; Guilherme D.; de Figueiredo; Celina M. H. "Kinetic heap-ordered trees: Tight analysis and improved algorithms" (PDF). Information Processing Letters. pp. 165–169. Archived from the original (PDF) on May 24, 2015. Retrieved May 17, 2012.
da Fonseca, Guilherme D. and de Figueiredo, Celina M. H. and Carvalho, Paulo C. P. "Kinetic hanger" (PDF). Information Processing Letters. pp. 151–157. Archived from the original (PDF) on May 24, 2015. Retrieved May 17, 2012.CS1 maint: multiple names: authors list (link)
Basch, J, Guibas, L. J., Ramkumar, G. D. (1997). "Sweeping lines and line segments with a heap". Proceedings of the thirteenth annual symposium on Computational geometry. SCG. ACM. pp. 469–471. Retrieved May 17, 2012.CS1 maint: multiple names: authors list (link)
K. H., Tarjan, R. and T. K. (2001). "Faster kinetic heaps and their use in broadcast scheduling" (PDF). Proc. 12th ACM-SIAM Symposium on Discrete Algorithms. ACM. pp. 836–844. Retrieved May 17, 2012.CS1 maint: multiple names: authors list (link)

Guibas, Leonidas. "Kinetic Data Structures - Handbook" (PDF). Archived from the original (PDF) on 2007-04-18. Retrieved May 17, 2012.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[mobile-1] Basch, J., Guibas, L. J., Hershberger, J (1997). "Data structures for mobile data". Proceedings of the eighth annual ACM-SIAM symposium on Discrete algorithms. SODA. Society for Industrial and Applied Mathematics. pp. 747–756. Retrieved May 17, 2012.CS1 maint: multiple names: authors list (link)

[heap_analysis-2] Fonseca; Guilherme D.; de Figueiredo; Celina M. H. "Kinetic heap-ordered trees: Tight analysis and improved algorithms" (PDF). Information Processing Letters. pp. 165–169. Archived from the original (PDF) on May 24, 2015. Retrieved May 17, 2012.

[hanger-3] Fonseca, Guilherme D. and de Figueiredo, Celina M. H. and Carvalho, Paulo C. P. "Kinetic hanger" (PDF). Information Processing Letters. pp. 151–157. Archived from the original (PDF) on May 24, 2015. Retrieved May 17, 2012.CS1 maint: multiple names: authors list (link)

[sweep-4] Basch, J, Guibas, L. J., Ramkumar, G. D. (1997). "Sweeping lines and line segments with a heap". Proceedings of the thirteenth annual symposium on Computational geometry. SCG. ACM. pp. 469–471. Retrieved May 17, 2012.CS1 maint: multiple names: authors list (link)

[tarjan-5] K. H., Tarjan, R. and T. K. (2001). "Faster kinetic heaps and their use in broadcast scheduling" (PDF). Proc. 12th ACM-SIAM Symposium on Discrete Algorithms. ACM. pp. 836–844. Retrieved May 17, 2012.CS1 maint: multiple names: authors list (link)