Kelvin functions
In applied mathematics, the Kelvin functions berν(x) and beiν(x) are the real and imaginary parts, respectively, of
where x is real, and Jν(z), is the νth order Bessel function of the first kind. Similarly, the functions kerν(x) and keiν(x) are the real and imaginary parts, respectively, of
where Kν(z) is the νth order modified Bessel function of the second kind.
These functions are named after William Thomson, 1st Baron Kelvin.
While the Kelvin functions are defined as the real and imaginary parts of Bessel functions with x taken to be real, the functions can be analytically continued for complex arguments xeiφ, 0 ≤ φ < 2π. With the exception of bern(x) and bein(x) for integral n, the Kelvin functions have a branch point at x = 0.
Below, Γ(z) is the gamma function and ψ(z) is the digamma function.
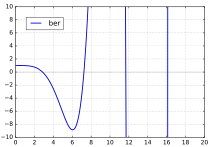
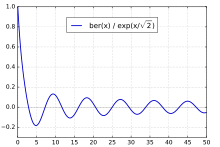
ber(x)
For integers n, bern(x) has the series expansion
where Γ(z) is the gamma function. The special case ber0(x), commonly denoted as just ber(x), has the series expansion
and asymptotic series
- ,
where
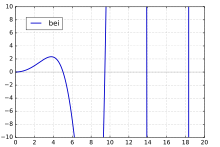
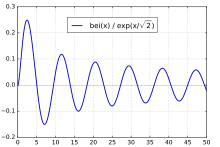
bei(x)
For integers n, bein(x) has the series expansion
The special case bei0(x), commonly denoted as just bei(x), has the series expansion
and asymptotic series
where α, , and are defined as for ber(x).
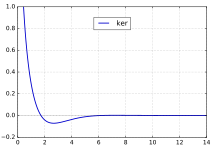
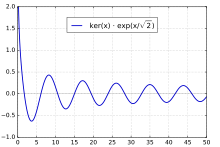
ker(x)
For integers n, kern(x) has the (complicated) series expansion
The special case ker0(x), commonly denoted as just ker(x), has the series expansion
and the asymptotic series
where
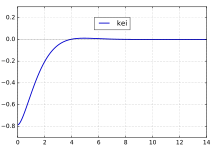
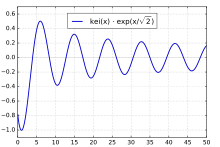
kei(x)
For integer n, kein(x) has the series expansion
The special case kei0(x), commonly denoted as just kei(x), has the series expansion
and the asymptotic series
where β, f2(x), and g2(x) are defined as for ker(x).
See also
References
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 9". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 379. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Olver, F. W. J.; Maximon, L. C. (2010), "Bessel functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248